广东省高考冲刺强化训练试卷十文科数学
集合P=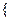 1,3,5,7,9,┅,2
1,3,5,7,9,┅,2 -1,┅
-1,┅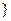
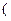
 ∈N
∈N
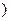 ,若
,若 ∈P,
∈P, ∈P时,
∈P时, □
□ ∈P,则运算□可能是( )
∈P,则运算□可能是( )
| A.加法 | B.减法 | C.乘法 | D.除法 |
把函数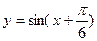 图象上各点的横坐标缩短到原来的
图象上各点的横坐标缩短到原来的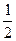 倍(纵坐标不变),再将图象向右平移
倍(纵坐标不变),再将图象向右平移 个单位,那么所得图象的一条对称轴方程为 ( )
个单位,那么所得图象的一条对称轴方程为 ( )
A. |
B. |
C. |
D. |
空间两直线 在平面
在平面 上射影分别为
上射影分别为 和
和 ,若
,若 ,
, 与
与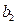 交于一点,则
交于一点,则 和
和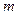 的位置关系为( )
的位置关系为( )
| A.一定异面 | B.一定平行 | C.异面或相交 | D.平行或异面 |
已知: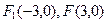 , 满足条件
, 满足条件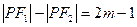 的动点P的轨迹是双曲线的一支,则
的动点P的轨迹是双曲线的一支,则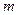 可以是下列数据中的①2; ②
可以是下列数据中的①2; ②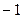 ; ③4; ④
; ③4; ④ ( )
( )
| A.①③ | B.①② | C.①②④ | D.②④ |
对任意实数 ,定义运算
,定义运算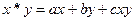 ,其中
,其中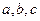 为常数,等号右边的运算是通常意义的加、乘运算.现已知
为常数,等号右边的运算是通常意义的加、乘运算.现已知 ,且有一个非零实数
,且有一个非零实数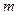 ,使得对任意实数
,使得对任意实数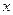 ,都有
,都有 ,则
,则 ( )
( )
| A.2 | B.3 | C.4 | D.5 |
某校有高级教师26人,中级教师104人,其他教师若干人.为了了解该校教师的工资收入情况,若按分层抽样从该校的所有教师中抽取56人进行调查,已知从其他教师中共抽取了16人,则该校共有教师 人.
(几何证明选讲选做题)如图,圆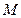 与圆
与圆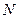 交于
交于 两点,
两点,
以 为切点作两圆的切线分别交圆
为切点作两圆的切线分别交圆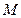 和圆
和圆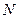 于
于 两点,延
两点,延
长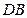 交圆
交圆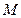 于点
于点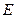 ,延长
,延长 交圆
交圆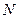 于点
于点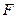 ,已知
,已知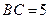 ,
, ,则
,则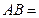 ;
;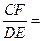 .
.
(本小题满分12分)在△ABC中,角A,B,C的对边分别为a,b,c,且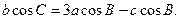
(1)求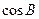 的值; (2)若
的值; (2)若 ,且
,且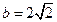 ,求
,求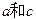 的值.
的值.
(本小题满分13分)某购物广场拟在五一节举行抽奖活动,规则是:从装有编号为0,1,2,3四个小球的抽奖箱中同时抽出两个小球,两个小球号码相加之和等于5中一等奖,等于4中二等奖,等于3中三等奖.
(1)求中三等奖的概率;
(2)求中奖的概率.
(本小题满分13分)如图,已知三棱柱 的所有棱长都相等,且侧棱垂直于底面,由
的所有棱长都相等,且侧棱垂直于底面,由 沿棱柱侧面经过棱
沿棱柱侧面经过棱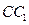 到点
到点 的最短路线长为
的最短路线长为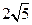 ,设这条最短路线与
,设这条最短路线与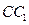 的交点为
的交点为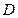 .
.
(1)求三棱柱 的体积;
的体积;
(2)在面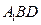 内是否存在过
内是否存在过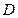 的直线与面
的直线与面 平行?证明你的判断;
平行?证明你的判断;
(3)证明:平面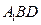 ⊥平面
⊥平面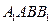 .
.
(本小题满分14分)设椭圆
 的左焦点为
的左焦点为 ,上顶点为
,上顶点为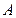 ,过点
,过点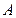 与
与 垂直的直线分别交椭圆
垂直的直线分别交椭圆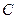 与
与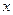 轴正半轴于点
轴正半轴于点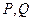 ,且
,且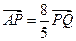 . ⑴求椭圆
. ⑴求椭圆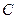 的离心率;⑵若过
的离心率;⑵若过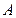 、
、 、
、 三点的圆恰好与直线
三点的圆恰好与直线
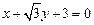 相切,求椭圆
相切,求椭圆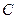 的方程.
的方程. 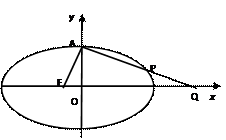
(本小题满分14分)2008年奥运会在中国举行,某商场预计2008年从1日起前 个月,顾客对某种奥运商品的需求总量
个月,顾客对某种奥运商品的需求总量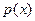 件与月份
件与月份 的近似关系是
的近似关系是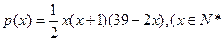 且
且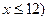 ,该商品的进价
,该商品的进价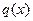 元与月份
元与月份 的近似关系是
的近似关系是 且
且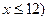 .
.
(1)写出今年第 月的需求量
月的需求量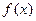 件与月份
件与月份 的函数关系式;
的函数关系式;
(2)该商品每件的售价为185元,若不计其他费用且每月都能满足市场需求,则此商场
今年销售该商品的月利润预计最大是多少元?
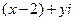 和
和 是共轭复数,则实数
是共轭复数,则实数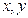 的值是( )
的值是( )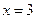 且
且
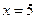 且
且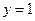
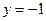
 且
且 相切于
相切于 处的切线方程是(其中
处的切线方程是(其中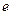 是自然对数的底)( )
是自然对数的底)( )

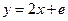
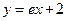
 的夹角为
的夹角为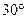 的单位向量是( )
的单位向量是( )
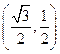
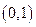 或
或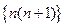 中的一项( )
中的一项( ) 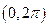 内,使
内,使 成立的
成立的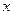 的取值范围是( )
的取值范围是( )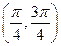
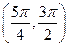
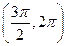
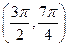
 ,则判断框中应填入的条件是 .
,则判断框中应填入的条件是 .
 是
是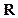 上的奇函数,
上的奇函数, ,且对任意
,且对任意 都
都 成立,则
成立,则 ,
, .
. 与曲线
与曲线
 (
(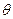 为参数)没有公共点,则实数
为参数)没有公共点,则实数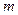 的取值范围是 .
的取值范围是 .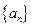 是以4为首项的正数数列,双曲线
是以4为首项的正数数列,双曲线 的一个焦点坐标为
的一个焦点坐标为 , 且
, 且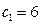 , 一条渐近线方程为
, 一条渐近线方程为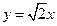 .
. 的通项公式;
的通项公式;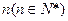 ,不等式
,不等式 是否恒成立?并说明理由.
是否恒成立?并说明理由. 粤公网安备 44130202000953号
粤公网安备 44130202000953号