安徽省安庆市十校初二第二学期期中考试
.如图所示,A、B、C分别表示三个村庄,AB=1000米,BC=600米,AC=800米,在新农村建设中,为了丰富群众生活,拟建一个文化活动中心,要求这三个村庄到活动中心的距离相等,则活动中心P的位置应该在( )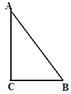
A.AB中点 B.BC中点 C.AC中点 D.∠C的平分线与AB的交点
.如图,已知在Rt△ABC中,∠BAC=90,AB=3,BC=5,若把Rt△ABC绕直接AC旋转一周,则所得圆锥的侧面积等于( )
| A.6π | B.9π | C.12π | D.15π |
古希腊著名的毕达哥拉斯派1、3、6、10、…这样的数称为“三角形数”,而把1、4、9、16…这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻的“三角形数”之和,下列等式中,符合这一规律的是( )
| A.13="3+10" | B.25="9+16" | C.36="15+21" | D.49=18+31 |
△ABC是等腰三角形,AB=AC,∠A=36°
(1)利用尺规作B的角平分线BD,交AC于点D;(保留作图痕迹,不写作法)
(2)判断△ABC是否为等腰三角形,并说明理由.
设四边形ABCD是边长为1的正方形,以对角线AC为边作第二个正方形ACEF,再以对角线AE作第二个正方形AEGH,如此下去…
(1)记正方形ABCD的边长为 =1,按上述方法所作的正方形边长依次为
=1,按上述方法所作的正方形边长依次为 ,请求出
,请求出 的值;
的值;
(2)根据以上规律写出 的值.
的值.
某文具厂加工一种学生画图工具2500套,在加工了1000套后,采用了新技术,使每天的工作效率是原来的1.5倍,结果提前5天完成任务,求该文具厂原来每天加工多少套这种学生画图工具.
有一水库大坝的横截面是梯形ABCD,AD∥BC,EF为水库的水面,点E在DC上,某课题小组在老师带领下想测量水的深度,他们测得背水坡AB的长为12米,迎水坡DE的长为2米,∠BAD=135°,∠ADC=120°,求水深.(精确到0.1米, )
)
如图,AB为⊙O的直径,弦CD⊥AB,垂足为点M,AE切⊙O于点A,交BC的延长线于点E,连接AC.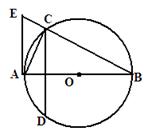
(1)若B=30°,AB=2,求CD的长;
(2)求证:AE2=EB·EC.
某电脑公司现有A、B、C三种型号的甲品牌电脑和D、E两种型号的乙品牌电脑,希望中学要从甲、乙两品牌电脑中各选一种型号的电脑。
(1)写出所有选购方案(利用树状图或列表法表示);
(2)如果(1)中各种选购方案被选中的可能性相同,那么A型号电脑被选中的概率是多少?
(3)现知希望中学购买甲、乙两种品牌电脑共36台(价格如右图所示),恰好用了10万元人民币,其中甲品牌电脑为A型电脑,求购买A型号电脑有几台?
已知,如图,在平行四边形ABCD中,AE是BC边上的高,将△ABE沿BC方向平移,使点E与点C重合,得△GFC.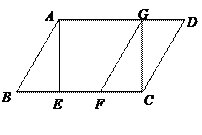
(1)求证:BE=DG;
(2)∠若B=60°,当AB与BC满足什么数量关系时,四边形ABFG是菱形?证明你的结论.
如图,抛物线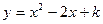 与x轴交于A、B两点,与y轴交于点C(0,-3)[图14(2)、图14(3)为解答备用图.
与x轴交于A、B两点,与y轴交于点C(0,-3)[图14(2)、图14(3)为解答备用图.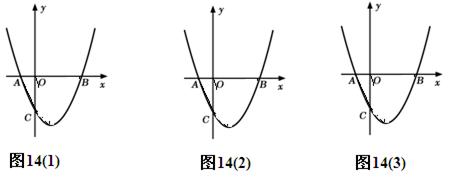
(1)k=_______,点A的坐标为___________,点C的坐标为_____________.
(2)设抛物线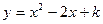 的顶点为M,求四边形ABMC的面积;
的顶点为M,求四边形ABMC的面积;
(3)在x轴下方的抛物线上是否存在一点D,使四边形ABDC的面积最大?若存在,请求出点D的坐标;若不存在,请说明理由.
已知等腰三角形的一条腰长是5,底边长是6,则它底边上的高为( )
| A.5 | B.3 | C.4 | D.7 |
关于x的方程(a -5)x2-4x-1=0有实数根,则a满足( )
| A.a≥1 | B.a>1且a≠5 | C.a≥1且a≠5 | D.a≠5 |
如果最简根式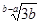 和
和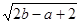 是同类二次根式,那么a、b的值是( )
是同类二次根式,那么a、b的值是( )
| A.a=0,b=2 | B.a=2,b=0 | C.a=-1,b=1 | D.a=1,b=-2 |
小明的作业本上有以下四题:①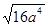 =4a2;②
=4a2;② ;
;
③ 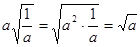 ;④
;④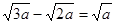 ,做错的题有( )
,做错的题有( )
| A.4个 | B.3个 | C.2个 | D.1个 |
一个直角三角形的斜边长比直角边长大2,另一直角边长为6,则斜边长为( )
| A.6 | B.8 | C.10 | D.12 |
如图,在Rt△ABC 中,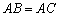 ,D、E是斜边BC上两点,且∠DAE=45°,将△
,D、E是斜边BC上两点,且∠DAE=45°,将△ 绕点
绕点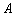 顺时针旋转90
顺时针旋转90 后,得到△
后,得到△ ,连接
,连接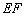 ,下列结论:①△
,下列结论:①△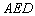 ≌△
≌△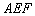 ; ②△
; ②△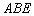 ≌△
≌△ ;
;
③ ; ④
; ④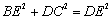 ,其中正确的是( )
,其中正确的是( )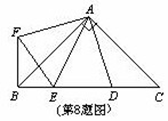
A.②④ B.①④ C.②③ D.①③
若关于x的方程x2-mx+3=0有实数根,则m的值可以为___(任意给出一个符合条件的值即可)
利用图(1)或图(2)两个图形中的有关面积的等量关系都能证明数学中一个十分著名的定理,这个定理称为 ,该定理的结论其数学表达式是 
已知 .甲、乙两个同学在
.甲、乙两个同学在 的条件下分别计算了
的条件下分别计算了 和
和 的值.甲说
的值.甲说 的值比
的值比 大,乙说
大,乙说 的值比
的值比 大.请你判断他们谁的结论是正确的,并说明理由.
大.请你判断他们谁的结论是正确的,并说明理由.
在国家下身的宏观调控下,某市的商品房成交价由今年3月分的14000元/ 下降到5月分的12600元/
下降到5月分的12600元/ ;
;
(1)问4、5两月平均每月降价的百分率是多少?(参考数据: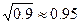 )
)
(2)如果房价继续回落,按此降价的百分率 ,你预测到7月分
,你预测到7月分 该市的商品房成交均价是否会跌破10000元/
该市的商品房成交均价是否会跌破10000元/ ?请说明理由。
?请说明理由。
如图,在ΔABC中,AB=AC=10,BC=8.用尺规作 图作BC边上的中线AD(保留作图痕迹,不要求写作法、证明),并求AD的长.
图作BC边上的中线AD(保留作图痕迹,不要求写作法、证明),并求AD的长. 

 的相反数是( )
的相反数是( )




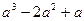 =_______________.
=_______________. (k为常数)有两个相等的实数根,则k=_______.
(k为常数)有两个相等的实数根,则k=_______.
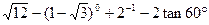
 ,其中
,其中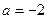

 (x>0)交于点A(3,m),与x轴交于点B.
(x>0)交于点A(3,m),与x轴交于点B.
 的结果是
的结果是

 在实数范围内有意义,则x的取值范围是( )
在实数范围内有意义,则x的取值范围是( ) 的两个解分别为
的两个解分别为 、
、 ,则
,则 的值为( )
的值为( )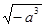 结果是 ( )
结果是 ( )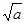
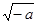
 中,
中, ,
, ,点
,点 为
为 的中点,
的中点,  于点
于点 ,则
,则 等于( )
等于( )




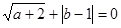 ,那么
,那么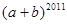 的值为 .
的值为 .

 …请你将发现的规律用含自然数n(n≥1)的等式表示出来 .
…请你将发现的规律用含自然数n(n≥1)的等式表示出来 .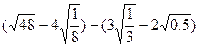

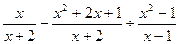 ,其中
,其中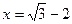
 的一元二次方程
的一元二次方程 有实数根
有实数根 .
. ,求t的最小值。
,求t的最小值。 粤公网安备 44130202000953号
粤公网安备 44130202000953号