[江西]2013届江西南昌高三第二次模拟突破冲刺文科数学试卷
椭圆 的左焦点为F,右顶点为A,以FA为直径的圆经过椭圆的上顶点,则椭圆的离心率为( )
的左焦点为F,右顶点为A,以FA为直径的圆经过椭圆的上顶点,则椭圆的离心率为( )
A. |
B. |
C. |
D. |
来源:2013届江西南昌高三第二次模拟突破冲刺文科数学试题
某次数学测试中,学号为i(i=1,2,3)的三位学生的考试成绩 则满足
则满足 的学生成绩情况的概率是
的学生成绩情况的概率是
A. |
B. |
C. |
D. |
来源:2013届江西南昌高三第二次模拟突破冲刺文科数学试题
△ABC的三个角的正弦值对应等于△A1B1C1的三个角的余弦值,在△ABC中,角A、B、C的对边分别为 、
、 、
、 ,且角A、B是△ABC中的两个较小的角,则下列结论中正确的是 .(写出所有正确结论的编号)
,且角A、B是△ABC中的两个较小的角,则下列结论中正确的是 .(写出所有正确结论的编号)
①△A1B1C1是锐角三角形;②△ABC是钝角三角形;③sinA>cosB
④
⑤若c=4,则ab<8.
来源:2013届江西南昌高三第二次模拟突破冲刺文科数学试题
已知 中,
中, 是三个内角
是三个内角 的对边,关于
的对边,关于 的
的
不等式 的解集是空集。
的解集是空集。
(1)求角 的最大值;
的最大值;
(2)若 ,
, 的面积
的面积 ,求当角
,求当角 取最大值时
取最大值时 的值。
的值。
来源:2013届江西南昌高三第二次模拟突破冲刺文科数学试题
从某节能灯生产在线随机抽取100件产品进行寿命试验,按连续使用时间(单位:天)共分5组,得到频率分布直方图如图.
(I)以分组的中点资料作为平均数据,用样本估计该生产线所生产的节能灯的预期连续使用寿命;
(II)为了分析使用寿命差异较大的产品,从使用寿命低于200天和高于350天的产品中用分层抽样的方法共抽取6件,求样品A被抽到的概率。
来源:2013届江西南昌高三第二次模拟突破冲刺文科数学试题
已知椭圆 的左焦点F为圆
的左焦点F为圆 的圆心,且椭圆上的点到点F的距离最小值为
的圆心,且椭圆上的点到点F的距离最小值为 。
。
(I)求椭圆方程;
(II)已知经过点F的动直线 与椭圆交于不同的两点A、B,点M(
与椭圆交于不同的两点A、B,点M( ),证明:
),证明: 为定值。
为定值。
来源:2013届江西南昌高三第二次模拟突破冲刺文科数学试题
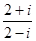 表示复平面内点位于( )
表示复平面内点位于( )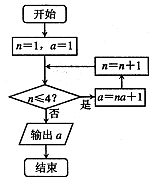
 中有
中有 ,数列
,数列 是等差数列,且
是等差数列,且 ,则
,则 ( )
( )




 的图像恒过定点A,且点A在直线
的图像恒过定点A,且点A在直线 上
上 ,则
,则 的最小值为( )
的最小值为( ) 部分图像如图所示,则函数表达式为:( )
部分图像如图所示,则函数表达式为:( )




 内部一点,
内部一点, 则
则 的面积为( )
的面积为( ) 



 的最小值为
的最小值为 ,若函数
,若函数 的解集为
的解集为



 则
则 .
. 的零点属于区间
的零点属于区间 ,则
,则 .
. 是坐标原点,点
是坐标原点,点 的坐标为(2,1),若点
的坐标为(2,1),若点 为平面区域
为平面区域 上的一个动点,则
上的一个动点,则 ·
· 的最大值是 。
的最大值是 。 在向量
在向量 上的投影为2,且
上的投影为2,且 与
与 ,则
,则 = 。
= 。 为等差数列,且
为等差数列,且
 的通项公式;
的通项公式; …
… .
. ⊥平面
⊥平面 ,
, ,
, ,
, ,
, ,
, ,
, ,
, 是
是 的中点.
的中点.
 平面
平面 ;
; ;
;
 在x=1处与直线
在x=1处与直线 相切.
相切. ,
, 的值;②求函数
的值;②求函数 在
在 上的最大值.
上的最大值. 时,若不等式
时,若不等式 对所有的
对所有的 都成立,求实数
都成立,求实数 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号