河北省高三年级秦皇岛市三区四县联考文科试题
(文)已知函数f(x)的导数为f′(x),若f′(x)<0(a <x <b)且f(b)>0,则在(a,b)内必有( )
| A.f(x)=0 | B.f(x)>0 | C.f(x)<0 | D.不能确定 |
(文)某网站欲调查网民对当前网页的满意程度,在登录的所有网民中,收回有效帖子共50000份,其中持各种态度的份数如下表所示.
| 很满意 |
满意 |
一般 |
不满意 |
| 10800 |
12400 |
15600 |
11200 |
为了了解网民的具体想法和意见,以便决定如何更改才能使网页更完美,打算从中抽选500份,为使样本更具有代表性,则在“满意”态度中要抽取( )
A.108 B.124 C.156 D.112
(文)曲线f(x)=x3+x-2在p0点处的切线平行于直线y=4x-1,则p0点的坐标为( )
| A.(-1,0) | B.(0,-2) |
| C.(-1,-4)或(1,0) | D.(1,4) |
二次函数f(x)=ax2+bx+c对一切x∈R,满足f(1-x)=f(1+x),且f(-1)<0,f(0)>0,则( )
| A.a+b+c<0 | B.b<a+c | C.c<2b | D.a,b,c均大于0 |
(文)已知一组数据x1,x2,x3,x4,x5的平均数是=2,方差是,那么另一组数据
3x1-2, 3x2-2, 3x3-2, 3x4-2, 3x5-2的平均数和方差分别为( )
| A.2, | B.2,1 | C.4, | D.4,3 |
若不等式x4-4x3>2-a对于实数x∈[-1,4]恒成立,则实数a的取值范围是( )
| A.[29,+∞) | B.(29,+∞) | C.(-∞,-27) | D.(-25,+∞) |
设命题p:不等式()x+4>m>2x-x2对一切实数x恒成立;命题q:函数
f(x)=-(7-2m)x是R上的减函数.若命题p或q为真命题,命题p且q为假命题,则实数m的取值范围是( )
A (1 ,4] B.[3 ,4]∪(-∞,1)
C.[3 ,4]∪(-∞,1] D.(-∞,4]
已知f(x)是定义在R上的偶函数,对任意的x∈R都有f(x+4)=f(x)+f(2)成立.若f(0)=0,f(1)=2,则f(1) +f(2)+f(3)+…+f(2007)的值等于( )
| A.2007 | B.2008 | C.2009 | D.2010 |
某路段检查站监控录象显示,在某时段内,有1000辆汽车通过该站,现在随机抽取其中的200辆汽车进行车速分析,分析的结果表示为右图的频率分布直方图,则估计在这一时段内通过该站的汽车中速度不小于90km/h的约有 辆.
(本小题满分10分)
已知奇函数f(x)=
(1)求实数m的值,并在给出的直角坐标系中画出函数
y=f(x)的图象;
(2)若函数f(x)在区间[-1,|a|-2]上单调递增,试
确定a的取值范围.
(本小题满分12分)
已知f(x)=-3x2+a(6-a)x+b.
(1)解关于a的不等式f(1)>0;
(2)当不等式f(x)>0的解集为(―1,3)时,求实数a,b的值.
(文)已知7件产品中有4件正品和3件次品.
(1)从这7件产品中一次性随机抽出3件,求抽出的产品中恰有1件正品数的概率;
(2)从这7件产品中一次性随机抽出4件,求抽出的产品中正品件数不少于次品件数的概率.
(文)某汽车生产企业上年度生产一品牌汽车的投入成本为10万元/辆,出厂价为13万元/辆,年销售量为5000辆.本年度为适应市场需求,计划提高产品档次,适当增加投入成本,若每辆车投入成本增加的比例为x(0<x<1),则出厂价相应提高的比例为0.7x,年销售量也相应增加.已知年利润=(每辆车的出厂价-每辆车的投入成本)×年销售量.
(1)若年销售量增加的比例为0.4x,为使本年度的年利润比上年度有所增加,则投入成本增加的比例x应在什么范围内?
(2)年销售量关于x的函数为y=3240(-x2+2x+),则当x为何值时,本年度的年利润最大?最大利润为多少?
(文)已知函数f(x)=-x3+ax2+bx+c图像上的点P(1,-2)处的切线方程为y=-3x+1.
(1)若函数f(x)在x=-2时有极值,求f(x)的表达式;
(2)函数f(x)在区间[-2,0]上单调递增,求实数b的取值范围.
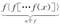 ,已知f(x)= .
,已知f(x)= . 粤公网安备 44130202000953号
粤公网安备 44130202000953号