2013年初中数学单元提优测试卷-图形的全等
如图,已知点A、D、C、F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件是( )
A. ∠BCA=∠F B. ∠B=∠E C. BC∥EF D. ∠A=∠EDF
如图,AE⊥AB且AE=AB,BC⊥CD且BC=CD,请按照图中所标注的数据,计算图中实线所围成的图形的面积S是( )
| A.50 | B.62 | C.65 | D.68 |
如图,已知△ABC中,∠ABC=45°,AC=4,H是高AD和BE的交点,则线段BH的长度为( )
A.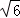 |
B.4 | C.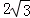 |
D.5 |
命题①邻补角互补;②对顶角相等;③同旁内角互补;④两点之间线段最短;⑤直线都相等;⑥任何数都有倒数;⑦如果a2=b2,那么a=b;⑧三角对应相等的两三角形全等;⑨如果∠A+∠B=90°,那么∠A与∠B互余.其中真命题有…( )
| A.3个 | B.4个 | C.5个 | D.6个 |
下列说法中不正确的是( )
| A.全等三角形的周长相等 | B.全等三角形的面积相等 |
| C.全等三角形能重合 | D.全等三角形一定是等边三角形 |
如图所示,∠1=∠2,AE⊥OB于E,BD⊥OA于D,交点为C,则图中全等三角形共有( )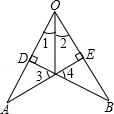
| A.2对 | B.3对 | C.4对 | D.5对 |
给出下列各命题:
①有两边和它们的夹角对应相等的两个三角形一定全等;
②有两边和一角对应相等的两个三角形一定全等;
③有两条直角边对应相等的两个直角三角形一定全等;
④有两条边分别相等的两个直角三角形一定全等;
其中假命题共有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
下列不能判定三角形全等的是( )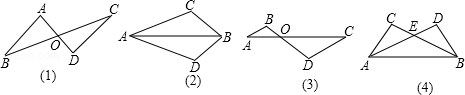
A.如图(1),线段AD与BC相交于点O,AO=DO,BO=CO.△ABO与△BCO
B.如图(2),AC=AD,BC=BD.△ABC与△ABD
C.如图(3),∠A=∠C,∠B=∠D.△ABO与△CDO
D.如图(4),线段AD与BC相交于点E,AE=BE,CE=DE,AC=BD.△ABC与△BAD
如图,AC=DF,∠ACB=∠DFE,点B、E、C在一条直线上,则下列条件中不能断定△ADC≌DEF的是( )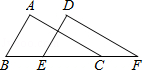
A. ∠A=∠D B. BE=CF C. AB=DE D. AB∥DE
下列条件中能判定△ABC≌△DEF的是( )
| A.AB=DE,BC=EF,∠A=∠D | B.∠A=∠D,∠B=∠E,∠C=∠F |
| C.AC=DF,∠B=∠F,AB=DE | D.∠B=∠E,∠C=∠F,AC=DF |
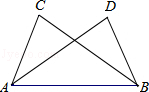
如图,在△ABC和△BAD中,若∠C=∠D,再添加一个条件,就可以判定△ABC≌△BAD你添加的条件是 .
如图,已知AB=AC,D为∠BAC的角平分线上面一点,连接BD,CD;如图2,已知AB=AC,D、E为∠BAC的角平分线上面两点,连接BD,CD,BE,CE;如图3,已知AB=AC,D、E、F为∠BAC的角平分线上面三点,连接BD,CD,BE,CE,BF,CF;…,依次规律,第n个图形中有全等三角形的对数是 .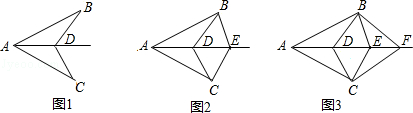
如图,将标号为A,B,C,D的正方形沿图中的虚线剪开后,得到标号为N,P,Q,M的四个图形,试按照“哪个正方形剪开后与哪个图形”的对应关系填空:A与 对应;B与 对应;C与 对应;D与 对应.
如图,如果△ABC≌△DEF,△DEF周长是32cm,DE=9cm,EF=13cm,∠E=∠B,则AC= cm.
如图EB交AC于M,交FC于D,AB交FC于N,∠E=∠F=90°,∠B=∠C,AE=AF.给出下列结论:①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN.其中正确的结论有 (填序号).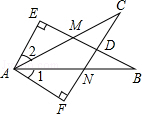
如图,已知CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD交于点O,且AO平分∠BAC,那么图中全等三角形共有 对.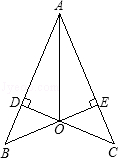
如图,在△ABC中,已知∠DBC=60°,AC>BC,又△ABC′、△BCA′、△CAB′都是△ABC形外的等边三角形,而点D在AC上,且BC=DC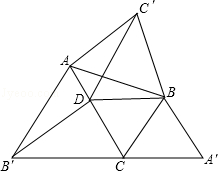
(1)证明:△C′BD≌△B′DC;
(2)证明:△AC′D≌△DB′A;
(3)对△ABC、△ABC′、△BCA′、△CAB′,从面积大小关系上,你能得出什么结论?
如图,已知:△ABC中,∠ACB=90°,D为AC边上的一点,E为DB的中点,CE的延长线交AB于点F,FG∥BC交DB于点G.试说明:∠BFG=∠CGF.
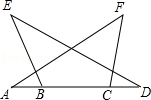
如图(1),A,E,F,C在一条直线上,AE=CF,过E,F分别作DE⊥AC,BF⊥AC,若AB=CD,试证明BD平分EF,若将△DEC的边EC沿AC方向移动变为图(2)时,其余条件不变,上述结论是否成立?请说明理由.
如图,两个全等的直角三角形△ABC和△A1B1C1中,∠ACB=∠A1C1B1=90°,两条相等的直角边AC,A1C1在同一直线上,A1B1与AB交于O,AB与B1C1交于E1,A1B1与BC交于E.
(1)写出图中除△ABC≌△A1B1C1外的所有其它各组全等三角形(不再连线和标注字母);
(2)求证:B1E1=BE.
(1)在图1中,已知∠MAN=120°,AC平分∠MAN.∠ABC=∠ADC=90°,则能得如下两个结论:①DC=BC;②AD+AB=AC.请你证明结论②;
(2)在图2中,把(1)中的条件“∠ABC=∠ADC=90°”改为∠ABC+∠ADC=180°,其他条件不变,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
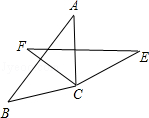
如图,点E在△ABC外部,点D在边BC上,DE交AC于F.若∠1=∠2=∠3,AC=AE,请说明△ABC≌△ADE的道理.
用两个全等的等边三角形△ABC和△ACD拼成菱形ABCD.把一个含60°角的三角尺与这个菱形叠合,使三角尺的60°角的顶点与点A重合,两边分别与AB,AC重合.将三角尺绕点A按逆时针方向旋转.
(1)当三角尺的两边分别与菱形的两边BC,CD相交于点E,F时,(如图1),通过观察或测量BE,CF的长度,你能得出什么结论并证明你的结论;
(2)当三角尺的两边分别与菱形的两边BC,CD的延长线相交于点E,F时(如图2),你在(1)中得到的结论还成立吗?简要说明理由.
已知:如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连接DH与BE相交于点G.
(1)求证:BF=AC;
(2)求证:CE= BF;
BF;
(3)CE与BG的大小关系如何?试证明你的结论.



 粤公网安备 44130202000953号
粤公网安备 44130202000953号