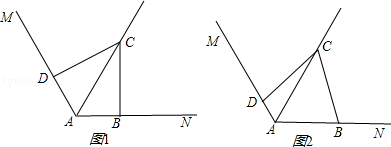（1）在图1中，已知∠MAN=120°，AC平分∠MAN．∠ABC=∠ADC=90°，则能得如下两个结论：①DC=BC；②AD+AB=AC．请你证明结论②；
（2）在图2中，把（1）中的条件“∠ABC=∠ADC=90°”改为∠ABC+∠ADC=180°，其他条件不变，则（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由．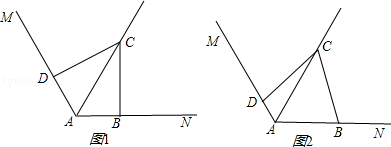
，4
相关知识点
推荐套卷
（1）在图1中，已知∠MAN=120°，AC平分∠MAN．∠ABC=∠ADC=90°，则能得如下两个结论：①DC=BC；②AD+AB=AC．请你证明结论②；
（2）在图2中，把（1）中的条件“∠ABC=∠ADC=90°”改为∠ABC+∠ADC=180°，其他条件不变，则（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由．
粤公网安备 44130202000953号