广东省汕头一模(数学理)试题
下列命题不正确的是
A.如果一个平面内的一条直线垂直于另一个平面内的任意直线,则两平面垂直;
B.如果一个平面内的任一条直线都平行于另一个平面,则两平面平行;
C.如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行;
D.如果两条不同的直线在一平面内的射影互相垂直,则这两条直线垂直.
已知某射击运动员,每次击中目标的概率都是 .现采用随机模拟的方法估计该运动员射击4次,至少击中3次的概率:先由计算器算出0到9之间取整数值的随机数,指定0,1,表示没有击中目标,2,3,4,5,6,,7,8,9表示击中目标;因为射击4次,故以每4个随机数为一组,代表射击4次的结果.经随机模拟产生了20组随机数:
.现采用随机模拟的方法估计该运动员射击4次,至少击中3次的概率:先由计算器算出0到9之间取整数值的随机数,指定0,1,表示没有击中目标,2,3,4,5,6,,7,8,9表示击中目标;因为射击4次,故以每4个随机数为一组,代表射击4次的结果.经随机模拟产生了20组随机数:
5727 0293 7140 9857 0347 4373 8636 9647 1417 4698
0371 6233 2616 8045 6011 3661 9597 7424 6710 4281
据此估计,该射击运动员射击4次至少击中3次的概率为
A.0.85 B.0.8192 C.0.8 D. 0.75
佛山某家电企业要将刚刚生产的100台变频空调送往市内某商场,现有4辆甲型货车和8辆乙型货车可供调配。每辆甲型货车的运输费用是400元,可装空调20台,每辆乙型货车的运输费用是300元,可装空调10台,若每辆车至多运一次,则企业所花的最少运费为
A.2000元 B.2200元 C.2400元 D.2800元
将侧棱相互垂直的三棱锥称为“直角三棱锥”,三棱锥
的侧面和底面分别叫直角三棱锥的“直角面和斜面”;过三棱锥顶点及斜面任两边中点的截面均称为斜面的“中面”.已知直角三角形具有性质:“斜边的中线长等于斜边边长的一半”.仿照此性质写出直角三棱锥具有的性质: .
某校从参加高一年级期中考试的学生中随机抽出 名学生,将其数学成绩(均为整数)分成六段
名学生,将其数学成绩(均为整数)分成六段 ,
, …
… 后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
(Ⅰ)求分数在 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;
(Ⅱ)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计本次考试的平均分;
(Ⅲ)若从 名学生中随机抽取
名学生中随机抽取 人,抽到的学生成绩在
人,抽到的学生成绩在 记
记 分,在
分,在 记
记 分,在
分,在 记
记 分,用
分,用 表示抽取结束后的总记分,求
表示抽取结束后的总记分,求 的分布列和数学期望.
的分布列和数学期望.
某学校拟建一座长 米,宽
米,宽 米的长方形体育馆.按照建筑要求,每隔
米的长方形体育馆.按照建筑要求,每隔 米需打建一个桩位,每个桩位需花费
米需打建一个桩位,每个桩位需花费 万元(桩位视为一点且打在长方形的边上),桩位之间的
万元(桩位视为一点且打在长方形的边上),桩位之间的 米墙面需花
米墙面需花 万元,在不计地板和天花板的情况下,当
万元,在不计地板和天花板的情况下,当 为何值时,所需总费用最少?
为何值时,所需总费用最少?
 ,
, ,函数
,函数 的定义域为
的定义域为 ,则
,则
 B.
B. C.
C. D.
D.
 ,则“
,则“ ”是“
”是“ ”的
”的 的离心率为
的离心率为 ,则双曲线的渐近线方程为
,则双曲线的渐近线方程为 B.
B. C.
C. D.
D.
 中,满足 “对
中,满足 “对 ,当
,当 时,都有
时,都有 ”的是
”的是 B.
B. C.
C. D.
D.
 (其中
(其中 )的图象如图所示,为了得到
)的图象如图所示,为了得到 的图像,则只要将
的图像,则只要将 的图像
的图像 
 个单位长度 B.向右平移
个单位长度 B.向右平移 个单位长度
个单位长度 的值是 .
的值是 . 满足:
满足: ,
, 项和为
项和为 ,则
,则 .
. ,则运行程序输出的结果为 .
,则运行程序输出的结果为 . 
 ,有
,有 ,则
,则 的值为__________.
的值为__________.
 (
( 为参数),
为参数),
 (
( 为参数).若曲线
为参数).若曲线 、
、 有公共点,则实数
有公共点,则实数 的取值范围____________.
的取值范围____________. 是圆
是圆 上的点,且
上的点,且 ,则
,则 对应的劣弧长为 .
对应的劣弧长为 .
 ,
, .向量
.向量 ,
, ,
,

 .
. ;
; ,
, ,求
,求 的值.
的值. 中,底面
中,底面 是边长为
是边长为 的正方形,
的正方形, 为
为 与
与 的交点,
的交点, ,
, 是线段
是线段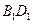 的中点.
的中点. 平面
平面 ;
; 平面
平面 ;
; 的大小.
的大小.
 (
( ),过点
),过点 作抛物线
作抛物线 的切线,切点分别为
的切线,切点分别为 、
、 (其中
(其中 ).
). 与
与 的值(用
的值(用 表示);
表示); 与直线
与直线 相切,求圆
相切,求圆 的前
的前 项和为
项和为 ,且
,且 (
( N*),其中
N*),其中 .
. (
( N*).
N*). ;
; .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号