[湖南]2013届湖南省怀化市高三第一次模拟考试理科数学试卷
若 (
( 、
、 是实数,
是实数, 是虚数单位),则复数
是虚数单位),则复数 对应的点在
对应的点在
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
下列命题中错误的是
A.命题“若 ,则 ,则 ”的逆否命题是“若 ”的逆否命题是“若 ,则 ,则 ” ” |
B.对命题 : : ,使得 ,使得 ,则 ,则 则 则 |
C.已知命题p和q,若 q为假命题,则命题p与q中必一真一假 q为假命题,则命题p与q中必一真一假 |
D.若 、 、 ,则“ ,则“ ”是“ ”是“ ”成立的充要条件 ”成立的充要条件 |
过双曲线 的右焦点
的右焦点 作圆
作圆 的切线
的切线 (切点为
(切点为 ),交
),交 轴于点
轴于点 .若
.若 为线段
为线段 的中点,则双曲线的离心率为
的中点,则双曲线的离心率为
| A.2 | B. |
C. |
D. |
在二项式 的展开式中,前三项的系数成等差数列,把展开式中所有的项重新排成一列,则有理项都不相邻的概率为
的展开式中,前三项的系数成等差数列,把展开式中所有的项重新排成一列,则有理项都不相邻的概率为
A. |
B. |
C. |
D. |
设曲线 的参数方程为
的参数方程为 (
( 是参数,
是参数, ),直线
),直线 的极坐标方程为
的极坐标方程为  ,若曲线
,若曲线 与直线
与直线 只有一个公共点,则实数
只有一个公共点,则实数 的值是 .
的值是 .
下列命题:
①当 时,
时, ;
;
② 是
是 成立的充分不必要条件;
成立的充分不必要条件;
③对于任意 的内角
的内角 、
、 、
、 满足:
满足: ;
;
④定义:如果对任意一个三角形,只要它的三边长 、
、 、
、 都在函数
都在函数 的定义域内,就有
的定义域内,就有 、
、 、
、 也是某个三角形的三边长,则称
也是某个三角形的三边长,则称 为“三角形型函数”.函数
为“三角形型函数”.函数 是“三角形型函数”.
是“三角形型函数”.
其中正确命题的序号为 .(填上所有正确命题的序号)
某商场为吸引顾客消费推出一项优惠活动,活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券,假定指针等可能地停在任一位置. 若指针停在 区域返券60元;停在
区域返券60元;停在 区域返券30元;停在
区域返券30元;停在 区域不返券. 例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.
区域不返券. 例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.
(1)若某位顾客消费128元,求返券金额不低于30元的概率;
(2)若某位顾客恰好消费280元,并按规则参与了活动,他获得返券的金额记为 (元),求随机变量
(元),求随机变量 的分布列和数学期望.
的分布列和数学期望.
如图1, ,
, ,过动点A作
,过动点A作 ,垂足
,垂足 在线段
在线段 上且异于点
上且异于点 ,连接
,连接 ,沿
,沿 将△
将△ 折起,使
折起,使 (如图2所示).
(如图2所示). 
(1)当 的长为多少时,三棱锥
的长为多少时,三棱锥 的体积最大;
的体积最大;
(2)当三棱锥 的体积最大时,设点
的体积最大时,设点 ,
, 分别为棱
分别为棱 、
、 的中点,试在棱
的中点,试在棱 上确定一点
上确定一点 ,使得
,使得
 ,并求
,并求 与平面
与平面 所成角的大小.
所成角的大小.
已知数列 的前
的前 项和为
项和为 ,点
,点 在直线
在直线 上.数列
上.数列 满足
满足 ,且
,且 ,前9项和为153.
,前9项和为153.
(1)求数列 、
、 {的通项公式;
{的通项公式;
(2)设 ,数列
,数列 的前
的前 和为
和为 ,求使不等式
,求使不等式 对一切
对一切 都成立的最大正整数
都成立的最大正整数 的值;
的值;
(3)设 ,问是否存在
,问是否存在 ,使得
,使得 成立?若存在,求出
成立?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
直角坐标平面上, 为原点,
为原点, 为动点,
为动点, ,
, . 过点
. 过点 作
作 轴于
轴于 ,过
,过 作
作 轴于点
轴于点 ,
, . 记点
. 记点 的轨迹为曲线
的轨迹为曲线 ,
,
点 、
、 ,过点
,过点 作直线
作直线 交曲线
交曲线 于两个不同的点
于两个不同的点 、
、 (点
(点 在
在 与
与 之间).
之间).
(1)求曲线 的方程;
的方程;
(2)是否存在直线 ,使得
,使得 ,并说明理由.
,并说明理由.
 ,
, ,则
,则 为
为



 ,则输入整数
,则输入整数 的最大值是
的最大值是
 ,其前
,其前 项和为
项和为 ,则点
,则点 所在的抛物线可能为
所在的抛物线可能为
 , 则
, 则 的值为
的值为



 的定义域为
的定义域为 ,则实数
,则实数 的取值范围是 .
的取值范围是 . 上一点
上一点 在直径
在直径 上的射影为
上的射影为 ,且
,且 ,
, ,则⊙
,则⊙

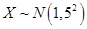 ,且
,且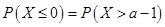 ,则实数
,则实数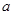 的值为 .
的值为 . 为
为 内一点,且
内一点,且 ,现随机将一颗豆子撒在
,现随机将一颗豆子撒在 内的概率为 .
内的概率为 . 上的区域
上的区域 由不等式组
由不等式组 给定. 若
给定. 若 为
为 的坐标为
的坐标为 ,则
,则 的最大值为 .
的最大值为 . 中,内角
中,内角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,且
,且
 的最大值.
的最大值. (
( ,
, 为自然对数的底数).
为自然对数的底数). 的最小值;
的最小值; 恒成立,求实数
恒成立,求实数 的值;
的值;
 粤公网安备 44130202000953号
粤公网安备 44130202000953号