2012年浙教版初中数学九年级上3.6圆锥的侧面积和全面积练习卷

一圆锥的侧面展开图的圆心角为120°，该圆锥的侧面积与全面积之比值为（     ）

A．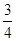

B．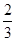

C．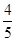

D．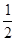

若圆锥经过轴的剖面是正三角形，则它的侧面积与底面积之比为（       ）

如图，将半径为2的圆形纸片沿半径OA、OB将其截成1：3两部分，用所得的扇形围成圆锥的侧面，则圆锥的底面半径为（     ）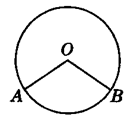

A．               B．1                C．1或3            D．或

如图，将三角形绕直线ι旋转一周，可以得到图所示的立体图形的是（     ）

在△ABC中，∠C=90°，AB=4cm，BC=3cm．若△ABC绕直线AC旋转一周得到一个几何体，则此几何体的侧面积是（     ）

将一个半径为8cm，面积为32πcm²的扇形铁皮围成一个圆锥形容器（不计接缝），那么这个圆锥形容器的高为（     ）

A．4

B．

C．

D．

已知圆锥的母线长是10cm，侧面展开图的面积是60πcm²，则这个圆锥的底面半径是     cm．

已知圆锥的底面半径是2cm，母线长是5cm，则它的侧面积是       ．

圆锥的轴截面是一个等边三角形，则这个圆锥的底面积、侧面积、全面积的比是       ．

一个扇形，半径为30cm，圆心角为120°，用它做成一个圆锥的侧面，那么这个圆锥的底面半径为       ．

一个扇形，半径为30cm，圆心角为120°，用它做成一个圆锥的侧面，那么这个圆锥的全面积为       ．

一个圆锥形的烟囱帽的侧面积为2000πcm²，母线长为50cm，那么这个烟囱帽的底面直径为（     ）

圆锥的高为3cm，底面半径为4cm，求它的侧面积和侧面展开图的圆心角．

以斜边长为a的等腰直角三角形的斜边为轴，旋转一周，求所得图形的表面积．

已知两个圆锥的锥角相等，底面面积的比为9：25，其中底面较小的圆锥的底面半径为6cm，求另一个圆锥的底面积的大小．

轴截面是顶角为120°的等腰三角形的圆锥侧面积和底面积的比是多少？

如图，已知圆锥的母线SB=6，底面半径r=2，求圆锥的侧面展开图扇形的圆心角α．

一个圆锥的底面半径为10cm，母线长20cm，求：
（1）圆锥的全面积；
（2）圆锥的高；
（3）轴与一条母线所夹的角；
（4）侧面展开图扇形的圆心角．

一个扇形如图，半径为30cm，圆心角为120°，用它做成一个圆锥的侧面，求圆锥底面半径和锥角．

一个圆锥的轴截面是等边三角形，它的高是．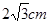
（1）求圆锥的侧面积和全面积；
（2）画出圆锥的侧面展开图．

若△ABC为等腰直角三角形，其中∠ABC=90°，AB=BC=5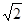cm，求将等腰直角三角形绕直线AC旋转一周所得到图形的面积．

用一块圆心角为300°的扇形铁皮做一个圆锥形烟囱帽，圆锥的底面直径为1m，求这个扇形铁皮的半径．

如图，粮仓的顶部是圆锥形，这个圆锥的底面周长为36m，母线长为8m，为防雨需在粮仓顶部铺上油毡，如果按用料的10%计接头重合部分，那么这座粮仓实际需用油毡的面积是多少？

如图，有一直径是1m的圆形铁皮，要从中剪出一个最大的圆心角是90°的扇形ABC，求：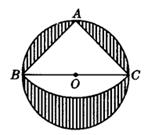

（1）被剪掉的阴影部分的面积；
（2）用所留的扇形铁皮围成一个圆锥，该圆锥的底面圆半径是多少？（结果可用根号表示）

小明要在半径为1m，圆心角为60°的扇形铁皮上剪取一块面积尽可能大的正方形铁皮．小明在扇形铁皮上设计了如图所示的甲、乙两种方案剪取所得的正方形的面积，并计算哪个正方形的面积较大？（估算时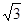取1.73，结果保留两个有效数字）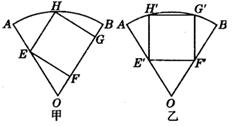

一个形如圆锥的冰淇淋纸筒，其底面直径为6cm，母线长为5cm，围成这样的冰淇淋纸筒所需纸片的面积是（     ）

圆锥可以看成是直角三角形以它的一条直角边所在的直线为轴，其余各边旋转一周而成的面所围成的几何体，那么圆台可以看成是               所在的直线为轴，其余各边旋转一周而成的面所围成的几何体；如果将一个半圆以它的直径所在的直线为轴旋转一周，所得的几何体应该是               ．

在半径为27m的广场中央，点O的上空安装了一个照明光源S，S射向地面的光束呈圆锥形，其轴截面SAB的顶角为120°（如图），求光源离地面的垂直高度SO．（精确到0.1m；=1.44，=1.732，=2.236，以上数据供参考）