[浙江]2013届浙江省新梦想新教育新阵地联谊学校高三回头考联考理科数学试卷
集合{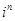 |
|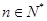 }(其中i是虚数单位)中元素的个数是( )
}(其中i是虚数单位)中元素的个数是( )
| A.1 | B.2 | C.4 | D.无穷多个 |
若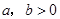 ,则
,则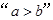 是“
是“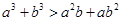 ”的( )
”的( )
| A.充分非必要条件 | B.必要非充分条件 |
| C.充分且必要条件 | D.既非充分也非必要条件 |
已知F1和F2分别是双曲线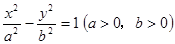 的左、右焦点,P是双曲线左支的一点,
的左、右焦点,P是双曲线左支的一点, 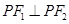 ,
,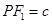 ,则该双曲线的离心率为( )
,则该双曲线的离心率为( )
A.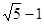 |
B.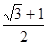 |
C.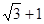 |
D.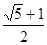 |
平行四边形ABCD中AC交BD于O,AC=5,BD=4,则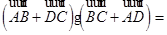 ( )
( )
| A.41 | B.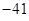 |
C.9 | D.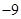 |
若关于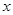 的不等式
的不等式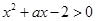 在区间
在区间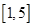 上有解,则实数
上有解,则实数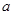 的取值范围为( )
的取值范围为( )
A.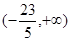 |
B.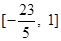 |
C.(1,+∞) | D.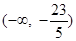 |
如图所示是某个区域的街道示意图(每个小矩形的边表示街道),那么从A到B的最短线路有( )条
| A.100 | B.400 |
| C.200 | D.250 |
棱长为2的正方体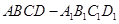 在空间直角坐标系中移动,但保持点A、B分别在x轴、y轴上移动,则点
在空间直角坐标系中移动,但保持点A、B分别在x轴、y轴上移动,则点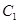 到原点O的最远距离为( )
到原点O的最远距离为( )
A.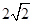 B.
B.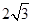 C.5 D.4
C.5 D.4
过抛物线 的焦点作一条倾斜角为
的焦点作一条倾斜角为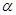 ,长度不超过8的弦,弦所在的直线与圆
,长度不超过8的弦,弦所在的直线与圆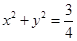 有公共点,则
有公共点,则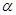 的取值范围是
的取值范围是
(本题14分)已知向量m =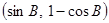 ,向量n =
,向量n =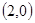 ,且m与n所成角为
,且m与n所成角为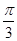 ,其中A、B、C是
,其中A、B、C是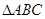 的内角。
的内角。
(Ⅰ)求角B的大小;
(Ⅱ)求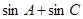 的取值范围。
的取值范围。
(本题14分)口袋内有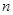 (
(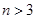 )个大小相同的球,其中有3个红球和
)个大小相同的球,其中有3个红球和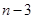 个白球.已知从
个白球.已知从
口袋中随机取出一个球是红球的概率是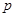 ,且
,且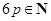 。若有放回地从口袋中连续地取四次球(每次只取一个球),在四次取球中恰好取到两次红球的概率大于
。若有放回地从口袋中连续地取四次球(每次只取一个球),在四次取球中恰好取到两次红球的概率大于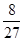 。
。
(Ⅰ)求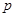 和
和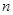 ;
;
(Ⅱ)不放回地从口袋中取球(每次只取一个球),取到白球时即停止取球,记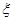 为第一次取到白球时的取球次数,求
为第一次取到白球时的取球次数,求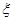 的分布列和期望
的分布列和期望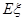 。
。
(本题15分)如图,在四棱锥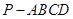 中,
中, 底面
底面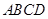 ,
,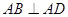 ,
,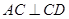 ,
,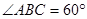 ,
,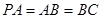 ,
,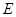 是
是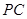 的中点。
的中点。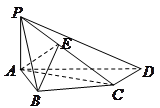
(Ⅰ)证明: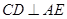 ;
;
(Ⅱ)证明: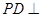 平面
平面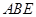 ;
;
(Ⅲ)求二面角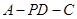 的正切值.
的正切值.
(本题15分)已知点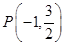 是椭圆E:
是椭圆E: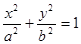 (
(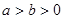 )上一点,F1、F2分别是椭圆E的左、右焦点,O是坐标原点,PF1⊥x轴.
)上一点,F1、F2分别是椭圆E的左、右焦点,O是坐标原点,PF1⊥x轴.
(Ⅰ)求椭圆E的方程;
(Ⅱ)设A、B是椭圆E上两个动点,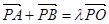 (
(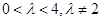 ).求证:直线AB的斜率为定值;
).求证:直线AB的斜率为定值;
(Ⅲ)在(Ⅱ)的条件下,当△PAB面积取得最大值时,求λ的值.
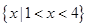 ,B=
,B=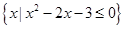 ,则
,则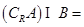 ( )
( )
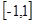
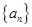 为等差数列,
为等差数列,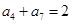 ,
,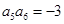 ,则
,则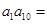 ( )
( )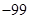
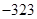
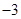
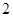
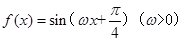 与函数
与函数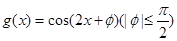 的对称轴完全相同,则
的对称轴完全相同,则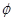 的值为( )
的值为( )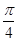
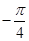
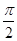
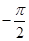

 展开式中二项式系数之和是1024,常数项为
展开式中二项式系数之和是1024,常数项为 ,则实数
,则实数 的值是
的值是  ,则输出的
,则输出的

 的前n项和为
的前n项和为 ,若数列
,若数列 是首项和公比都是3的等比数列,则
是首项和公比都是3的等比数列,则 _____
_____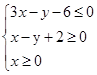 内的两个动点,向量
内的两个动点,向量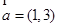 ,则
,则 的最大值是________
的最大值是________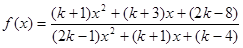 的定义域用D表示,则使
的定义域用D表示,则使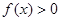 对
对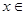 D均成立的实数
D均成立的实数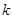 的范围是___
的范围是___ 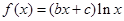 在
在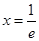 处取得极值,且在
处取得极值,且在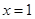 处的切线的斜率为1。
处的切线的斜率为1。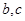 的值及
的值及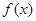 的单调减区间;
的单调减区间;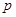 >0,
>0,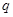 >0,
>0,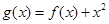 ,求证:
,求证: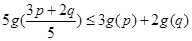 。
。 粤公网安备 44130202000953号
粤公网安备 44130202000953号