[江苏]2010-2011学年江苏省南通地区八年级上学期期末数学试卷
点M(-3,2)关于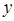 轴对称的点的坐标为
轴对称的点的坐标为
| A.(-3,-2) | B.(3,-2) | C.(3,2) | D.(-3,2) |
下列计算正确的是
| A.x2·x2=2x4 | B.(-2a)3= -8a3 | C.(a3)2=a5 | D.m3÷m3=m |
在长方形ABCD中,AB=2,BC=1,动点P从点B出发,沿路线B→C→D做匀速运动,那么△ABP的面积S与点P运动的路程x之间的函数图象大致为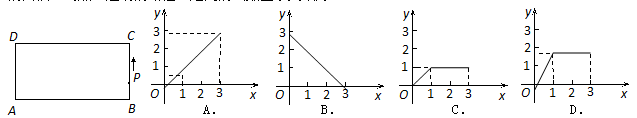
如图,在等腰△ABC中,∠BAC=120º,DE是AC 的垂直平分线,线段DE=1cm,则BD的长为
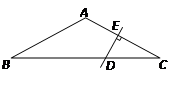
| A.6cm | B.8cm | C.3cm | D.4cm |
将直线 y ="2x" ─ 4 向上平移5个单位后,所得直线的表达式是____________.
已知木星的质量约是a×1024吨,地球的质量约是3a×1021吨,则木星的质量约是地球质量的___________倍.(结果取整数)
如图,在△ABC中,∠BAC=135º,AD⊥BC于D,且AB+BD=DC,那么∠C= °.
已知△ABC,利用直尺和圆规,根据下列要求作图(保留作图痕迹,不要求写作法)
并根据要求填空:
(1)作∠ABC的平分线BD交AC于点D;
(2)作线段BD的垂直平分线交AB于点E,交BC于点F.
由(1)、(2)可得:线段EF与线段BD的关系为 .
如图,已知△ABC的三个顶点在格点上.
(1)作出与△ABC关于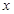 轴对称的图形△A1B1C1;
轴对称的图形△A1B1C1;
(2)求出△A1B1C1的面积.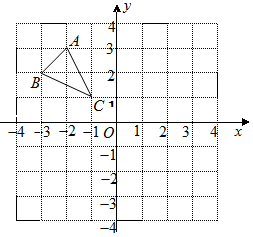
我们知道,随着海拔高度的上升,温度随之下降,且温度y(℃)是高出地面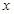 (千米)的一次函数.南通气象台某仪器显示,某时刻高出地面2千米处温度为8℃,高出地面5千米处温度为零下10℃.
(千米)的一次函数.南通气象台某仪器显示,某时刻高出地面2千米处温度为8℃,高出地面5千米处温度为零下10℃.
(1)写出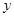 与
与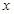 之间的函数关系式;
之间的函数关系式;
(2)就该时刻,求南通地区地面温度大约是多少℃?
(3)此刻,有一架飞机飞过南通上空,若机舱内仪表显示飞机外面的温度为-34℃,求飞机离地面的高度为多少千米?
如图,△ABC为等边三角形,点M是线段BC上的任意一点,点N是线段CA上任意一点,且BM=CN,直线BN与AM交于点Q.
(1)求证: △BAN≌△ACM
(2)求∠BQM的大小. 
已知动点 在函数
在函数 的图象上,且点P在第一象限,点A的坐标为(4,0),设△OPA的面积为S.
的图象上,且点P在第一象限,点A的坐标为(4,0),设△OPA的面积为S.
(1)用含 的解析式表示S,并求出
的解析式表示S,并求出 的取值范围;
的取值范围;
(2)求S=8时,点P的坐标.
仔细阅读下面例题,解答问题:
例题:已知二次三项式x2-4x+m有一个因式是(x+3),求另一个因式以及m的值。
解:设另一个因式为(x+n),得 x2-4x+m=(x+3)(x+n)
则 x2-4x+m=x2+(n+3)x+3n
∴
解得:n=-7, m=-21 ∴ 另一个因式为(x-7),m的值为-21
问题:仿照以上方法解答下面问题:
已知二次三项式2x2+3x-k有一个因式是(2x-5),求另一个因式以及k的值。
如图,已知BE⊥AD,CF⊥AD,且BE=CF.
(1)请你判断AD是△ABC的中线还是角平分线?并证明你的结论.
(2)在(1)的条件下,若AB=6,AC=4,请确定AD的值范围.
 、
、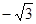 、
、 、π这五个数中,无理数有
、π这五个数中,无理数有 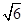


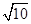
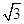
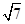
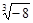 = .
= .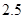
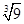 .
. = .
= . ,
, ,则
,则 ___________.
___________. 的图象如右图所示,则不等式0≤
的图象如右图所示,则不等式0≤ <5的解集为 .
<5的解集为 .
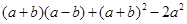 .
. 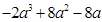 .
.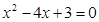 ,求
,求 的值.
的值. 轴交于点A,与
轴交于点A,与 轴交于点B,与直线OC:
轴交于点B,与直线OC: 交于点C.
交于点C. ,
,
 的平分线ON,若AB⊥ON,垂足为E,△OAC的面积为6,且OA=4,P、Q分别为线段OA、OE上的动点,连结AQ与PQ,试探索AQ+PQ是否存在最小值?若存在,求出这个最小值;若不存在,说明理由.
的平分线ON,若AB⊥ON,垂足为E,△OAC的面积为6,且OA=4,P、Q分别为线段OA、OE上的动点,连结AQ与PQ,试探索AQ+PQ是否存在最小值?若存在,求出这个最小值;若不存在,说明理由.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号