[江苏]2012届江苏镇江九年级5月中考模拟数学试卷

下列图形中，你认为既是中心对称图形又是轴对称图形的是（ ▲ ）

A．             B．              C．                    D．

一次函数y=kx+b的图象（如图），当x＜0时，y的取值范围是（ ▲ ）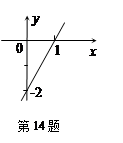

A．y＞0

B．y＜0

C．y＜2

D．2＜y＜0

如图所示，一只蚂蚁以均匀的速度沿台阶爬行，那么蚂蚁爬行的高度随时间变化的图象大致是（ ▲ ）

反比例函数的图象上有两点A（x₁,y₁），B（x₂，y₂）,且y₁＞y₂则（ ▲ ）

如图，等腰直角三角形ABC中，AC＝BC>3，点M在AC上，点N在CB的延长线上，MN交AB于点O，且AM＝BN＝3，则S_△AMO与S_△BNO的差是（ ▲ ）

A.9     B.4.5   C.0   D.因为AC、BC的长度未知，所以无法确定

25的平方根是      ▲      。]

已知的补角是120°，则tanA=    ▲     。

分解因式：      ▲      。

在函数y＝中，x的取值范围是     。

直线的图像与轴的交点坐标是    ▲  。

2011年年末我国总人口已经达到134735万人，这个数字用科学记数法可以表示为　　▲　 人；（保留3位有效数字）；

如图，等腰△ABC中，AB=AC，AD是底边BC上的高，若AB=5cm，BC=6cm，则
AB边上的高为    ▲    cm。

将抛物线的图像向右平移3个单位后，得到的新抛物线图像与y轴的交点坐标为 ▲   。

如图，把一个长方形纸片沿EF折叠后，点D、C分别落在D₁、C₁的位置．若∠EFB＝65°，则∠BFC₁=　　▲　　°。

一个叫巴尔末的瑞士中学教师成功地从光谱数据，，，，…中得到巴尔末公式，从而打开了光谱奥秘的大门，请你按照这种规律，写出第n（n≥1）个光谱数据是 __▲____．

如图所示:Rt△ABO中,直角边BO落在x轴负半轴上，点A的坐标是（－4，2），以O为位似中心，按比例尺1∶2，把△ABO缩小，则点A的对应点A′的坐标为__  ▲ ．

已知：直线（n为正整数）与两坐标轴围成的三角形面积为，则__  ▲     ．

计算：|－4|－(－1)⁰+2cos45°+
化简：（－)÷

解方程或不等式组：
解方程：
解不等式组：

已知：如图，在等腰梯形ABCD中，AD∥BC，AB＝DC，点E为边BC上一点，且AE＝DC。

求证：四边形AECD是平行四边形
当等腰梯形ABCD满足__  ▲ 时（添加一个条件），
则四边形AECD是菱形。

小张同学学完统计知识后，随机调查了她所在辖区若干名居民的年龄，将调查数据绘制成如下扇形统计图和条形统计图：


请根据以上不完整的统计图提供的信息，解答下列问题：
小张共调查了__ ▲ 名居民的年龄，图中＝_  ▲ ；
补全条形统计图，并注明人数
该辖区居民的年龄中位数在__  ▲ 年龄段
若该辖区年龄在60岁及以上的居民约有3000人，估计该辖区居民人数是__  ▲ 人。

如图：电路图上有四个开关A、B、C、D和一个小灯泡，闭合开关D或同时闭合开关A，B，C都可使小灯泡发光。

任意闭合其中一个开关，则小灯泡发光的概率等于__  ▲ ；
任意闭合其中两个开关，请用画树状图或列表的方法求出小
灯泡发光的概率．

如图，某人在山坡坡脚处测得电视塔尖点的仰角为，沿山坡向上走到处再测得点的仰角为，已知米，山坡坡度且O 、A、B在同一条直线上．求电视塔的高度以及此人所在位置点的铅直高度．（测倾器高度忽略不计，结果保留根号形式）

在8×8的正方形网格中建立如图所示的平面直角坐标系，已知A（2，4），B（4，2）．C是第一象限内的一个格点，由点C与线段AB组成一个以AB为底，且腰长为无理数的等腰三角形．

填空：C点的坐标是　▲　，△ABC的面积是　▲　
将△ABC绕点C旋转180°得到△A₁B₁C₁，连接AB₁、BA₁，试判断四边形AB₁A₁B是何种特殊四边形，请说明理由；
请探究：在x轴上是否存在这样的点P，使四边形ABOP的面积等于△ABC面积的2倍？若存在，请直接写出点P的坐标（不必写出解答过程）；若不存在，请说明理由．

如图，四边形ABCD内接于⊙O，BD是⊙O的直径，AE⊥CD，垂足为E，DA平分∠BDE

求证：AE是⊙O的切线
若∠DBC=30°，DE=1cm，求BD的长。

某商场试销一种成本为每件60元的服装，规定试销期间销售单价不低于成本单价，且获利不得高于45%，经试销发现，销售量 y（件）与销售单价x （元）符合一次函数y= ,
若该商场获得利润为w 元，试写出利润w 与销售单价x 之间的关系式；销售单价x定为多少元时，商场可获得最大利润，最大利润是多少元？
若该商场获得利润不低于500元，试确定销售单价的范围．

如图，在梯形ABCD中，AD∥BC，AD=3，DC=5，AB=4，∠B=45°．动点M从B点出发沿线段BC以每秒2个单位长度的速度向终点C运动；动点N同时从C点出发沿线段CD以每秒1个单位长度的速度向终点D运动．设运动的时间为t秒．
求BC的长
当MN∥AB时，求t的值
试探究：t为何值时，△MNC为等腰三角形．

如图，将一把直角三角板的直角顶点放置于原点O，两直角边与抛物线交于M、N两点，设M、N的横坐标分别为m、n（m﹥0，n﹤0）；请解答下列问题：
当m=1时，n=__ ▲ ； 当m=2时，n=__ ▲ 试猜想m与n满足的关系，并证明你猜想的结论。
连接M、N，若△OMN的面积为S，求S关于m的函数关系式。
当三角板绕点O旋转到某一位置时，恰好使得∠MNO=30°，此时过M作MA⊥x轴，垂足为A，求出△OMA的面积
当m=2时，抛物线上是否存在一点P使M、N、O、P四点构成梯形，若存在，直接写出所有满足条件的点P的坐标；若不存在，说明理由。