如图，某人在山坡坡脚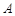
处测得电视塔尖点
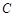的仰角为
，沿山坡向上走到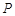
处再测得点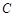的仰角为
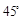，已知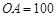
米，山坡坡度
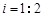且O 、A、B在同一条直线上．求电视塔
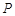的高度以及此人所在位置点的铅直高度．（测倾器高度忽略不计，结果保留根号形式）
x－mx＝5的解，求代数式
的值.
的方程组
的解满足
，求p的取值范围.
≤
的非负整数解.
＞－2相关知识点
推荐套卷
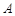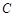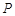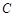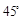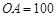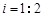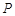如图，某人在山坡坡脚处测得电视塔尖点的仰角为，沿山坡向上走到处再测得点的仰角为，已知米，山坡坡度且O 、A、B在同一条直线上．求电视塔的高度以及此人所在位置点的铅直高度．（测倾器高度忽略不计，结果保留根号形式）
粤公网安备 44130202000953号