[四川]2012届四川省成都市高三第二次诊断性检测理科数学试卷
要使函数 在点x= -1处连续,则对f(x)可以补充的一个条件是
在点x= -1处连续,则对f(x)可以补充的一个条件是
A.当x="-1" 时,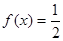 |
B.当x="-1" 时,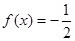 |
C.当x=l时,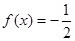 |
D.当 x=1 时,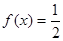 |
已知平面 //平面β,点
//平面β,点 ,直线
,直线 经过点A,则“
经过点A,则“ ”是“
”是“ //β"的
//β"的
| A.充要条件 | B.充分不必要条件 |
| C.必要不充分条件 | D.既不充分也不必要条件 |
设直线 (m为常数),圆
(m为常数),圆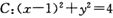 ,则
,则
| A.当m变化时,直线l恒过定点(-1,1); |
| B.直线l与圆C有可能无公共点 |
| C.若圆C上存在关于直线l对称的两点,则必有m=0 |
D.若直线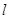 与圆C有两个不同交点M、N,则线段MN的长的最小值为 与圆C有两个不同交点M、N,则线段MN的长的最小值为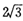 |
咱们“拼”了!拼车省时、省力、省心、省钱,“互助搭乘,绿色出行”.拼车主要分为:上下班拼车,过年、过节回家拼车,旅游拼车等.某高校的8名属“老乡”关系的同学准备拼车回家,其中大一、大二、大三、大四每个年级各两名,分乘甲、乙两辆汽车,每车限坐4名同学(乘同一辆车的4名同学不考虑位置),其中大一的孪生姐妹需乘同一辆车,则乘坐甲车的4名同学中恰有2名同学是来自于同一年级的乘坐方式共有
| A.18种 | B.24种 | C.36种 | D.48种 |
如图,三棱锥P—ABC内接于球0,PA丄平面ABC, 的外接圆为球O的小圆
的外接圆为球O的小圆 ,AB=1,PA=2.则下列结论正确的是
,AB=1,PA=2.则下列结论正确的是
A、 PC丄AB
B、点C到平面PAB的距离为2
C、该球的表面积为4
D、点B、C在该球上的球面距离为
已知A、B为椭圆 的左、右顶点,C(0,b),直线
的左、右顶点,C(0,b),直线 与X轴交于点D,与直线AC交于点P,且BP平分
与X轴交于点D,与直线AC交于点P,且BP平分 ,则此椭圆的离心率为
,则此椭圆的离心率为
A、
B、
C、
D、
已知函数. (m为常数),对任意
(m为常数),对任意 ,均有
,均有 恒成立.下列说法:
恒成立.下列说法:
①若 为常数)的图象关于直线x=1对称,则b=1;
为常数)的图象关于直线x=1对称,则b=1;
②若 ,则必有
,则必有 ;
;
③已知定义在R上的函数 对任意X均有
对任意X均有 成立,且当
成立,且当 时,
时, ;又函数
;又函数 (c为常数),若存在
(c为常数),若存在 使得
使得 成立,则c的取值范围是(-1,13).其中说法正确的个数是
成立,则c的取值范围是(-1,13).其中说法正确的个数是
| A.3个 | B.2个 | C.1个 | D.O个 |
已知曲线 满足在点
满足在点 处的切线与x轴平行,若将所有满足条件的切点的横坐标由小到大依次排列构成数列
处的切线与x轴平行,若将所有满足条件的切点的横坐标由小到大依次排列构成数列 ,则数列{xn}的前4项和为_______.
,则数列{xn}的前4项和为_______.
在空间直角坐标系O-xyz中, (其中i、j、k分别为X轴、y轴、z轴正方向上的单位向量).有下列命题:
(其中i、j、k分别为X轴、y轴、z轴正方向上的单位向量).有下列命题:
①若 且
且 ,则
,则
 的最小值为
的最小值为 ;
;
②设 ,若向量
,若向量 与k共线且
与k共线且 ,则动点P的轨迹是抛物线;
,则动点P的轨迹是抛物线;
③若 ,则平面MQR内的任意一点A (x,y,z)的坐标必然满足关系式
,则平面MQR内的任意一点A (x,y,z)的坐标必然满足关系式 ;
;
④设 ,
, ,若向量
,若向量 与j共线且
与j共线且 ,则动点P的轨迹是双曲线的一部分. 其中你认为正确的所有命题的序号为. _______
,则动点P的轨迹是双曲线的一部分. 其中你认为正确的所有命题的序号为. _______
已知 中,内角A、B、C所对边的长分别是a、b、c,且点
中,内角A、B、C所对边的长分别是a、b、c,且点 在直线
在直线 上.
上.
(I)求角C的大小;
(II)若 ,且A<B,求.
,且A<B,求. 的值.
的值.
如图,在四棱锥P—ABCD中,底面ABCD是边长为4的菱形,且 菱形ABCD的两条对角线的交点为O,PA=PC,PB=PD且PO= 3.点E是线段PA的中点,连接EO,EB,EC
菱形ABCD的两条对角线的交点为O,PA=PC,PB=PD且PO= 3.点E是线段PA的中点,连接EO,EB,EC
(I)证明:直线0E//平面PBC;
(II)求二面角E-BC-D的大小
“天宫一号”的顺利升空标志着我国火箭运载的技术日趋完善.据悉,担任“天宫一号”发射任务的是长征二号FT1火箭.为了确保发射万无一失,科学家对长征二号FT1运载火箭进行了170余项技术状态更改,增加了某项新技术.该项新技术要进入试用阶段前必须对其中三项不同指标甲、乙、丙进行通过量化检测.假设该项新技术的指标甲、乙、丙独立通过检测合格的概率分别为 ,指标甲、乙、丙检测合格分别记4分、2分、4分,若某项指标不合格,则该项指标记0分,各项指标检测结果互不影响.
,指标甲、乙、丙检测合格分别记4分、2分、4分,若某项指标不合格,则该项指标记0分,各项指标检测结果互不影响.
(I)求该项技术量化得分不低于8分的概率;
(II)记该项技术的三个指标中被检测合格的指标个数为随机变量 ,求
,求 的分布列与数学期望
的分布列与数学期望
已知数列{an}和{bn},b1=1,且 ,记
,记 .
.
(I)证明:数列{an}为等比数列;
(II)求数列{an}和{bn}的通项公式;
(III)记 ,数列{cn}的前n项和为Tn,若
,数列{cn}的前n项和为Tn,若 恒成立,求k的最大值.
恒成立,求k的最大值.
如图, 的顶点A、B为定点,P为动点,其内切圆O1与AB、PA、PB分别相切于点C、E、F,且
的顶点A、B为定点,P为动点,其内切圆O1与AB、PA、PB分别相切于点C、E、F,且 •
•
(I) 建立适当的平面直角坐标系,求动点p的轨迹w的方程;
(II) 设l是既不与AB平行也不与AB垂直的直线,线段AB的中点O到直线l的距离为 ,若l与曲线W相交于不同的两点G、H,点M满足
,若l与曲线W相交于不同的两点G、H,点M满足 ,证明:
,证明:

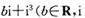 为虚数单位)是实数,则b=
为虚数单位)是实数,则b=  ,则
,则 =
= 



 ,且
,且 ,则集合B不可能是
,则集合B不可能是



 是等比数列,
是等比数列, ,则该数列前6项之积为
,则该数列前6项之积为  ,则
,则 的最小值为
的最小值为 
 ,若a//b,则实数t的值是_______.
,若a//b,则实数t的值是_______. 的值为. _______ (用数字作答)
的值为. _______ (用数字作答) ,,k为常数,e是自然对数的底数).
,,k为常数,e是自然对数的底数). 上的图象均在第一、二象限?若存在,求出k的最大值;若不存在,请说明理由;
上的图象均在第一、二象限?若存在,求出k的最大值;若不存在,请说明理由; ,记
,记 ,求证:
,求证:
 粤公网安备 44130202000953号
粤公网安备 44130202000953号