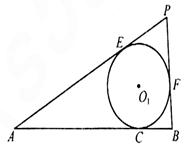
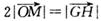如图，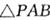
的顶点A、B为定点，P为动点，其内切圆O1与AB、PA、PB分别相切于点C、E、F，且
•
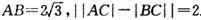(I) 建立适当的平面直角坐标系，求动点p的轨迹w的方程；
(II) 设l是既不与AB平行也不与AB垂直的直线,线段AB的中点O到直线l的距离为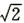
，若l与曲线W相交于不同的两点G、H，点M满足
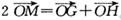，证明：
相关试题
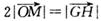
推荐套卷
如图，的顶点A、B为定点，P为动点，其内切圆O1与AB、PA、PB分别相切于点C、E、F，且 •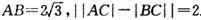
(I) 建立适当的平面直角坐标系，求动点p的轨迹w的方程；
(II) 设l是既不与AB平行也不与AB垂直的直线,线段AB的中点O到直线l的距离为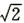，若l与曲线W相交于不同的两点G、H，点M满足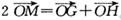，证明：
粤公网安备 44130202000953号