[北京]2012届北京市西城区高三4月第一次模拟考试文科数学
如图,在复平面内,复数 ,
, 对应的向量分别是
对应的向量分别是 ,
, ,则复数
,则复数 对应的点位于( )
对应的点位于( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
来源:2012届北京市西城区高三4月第一次模拟考试文科数学
已知正六棱柱的底面边长和侧棱长均为 ,其三视图中的俯视图如图所示,则其左视图的面积是( )
,其三视图中的俯视图如图所示,则其左视图的面积是( )
A. |
B. |
C. |
D. |
来源:2012届北京市西城区高三4月第一次模拟考试文科数学
设等比数列 的前
的前 项和为
项和为 .则“
.则“ ”是“
”是“ ”的( )
”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分又不必要条件 |
来源:2012届北京市西城区高三4月第一次模拟考试文科数学
某年级 名学生在一次百米测试中,成绩全部介于
名学生在一次百米测试中,成绩全部介于 秒与
秒与 秒之间.将测试结果分成
秒之间.将测试结果分成 组:
组: ,
, ,
, ,
, ,
, ,得到如图所示的频率分 布直方图.如果从左到右的
,得到如图所示的频率分 布直方图.如果从左到右的 个小矩形的面积之比为
个小矩形的面积之比为 ,那么成绩在
,那么成绩在 的学生人数是_____.
的学生人数是_____.
来源:2012届北京市西城区高三4月第一次模拟考试文科数学
如图,已知抛物线 及两点
及两点 和
和 ,其中
,其中 .过
.过 ,
, 分别作
分别作 轴的垂线,交抛物线于
轴的垂线,交抛物线于 ,
, 两点,直线
两点,直线 与
与 轴交于点
轴交于点 ,此时就称
,此时就称 ,
, 确定了
确定了 .依此类推,可由
.依此类推,可由 ,
, 确定
确定 ,
, .记
.记 ,
, .
.
给出下列三个结论:
① 数列 是递减数列;
是递减数列;
② 对 ,
, ;
;
③ 若 ,
, ,则
,则 .
.
其中,所有正确结论的序号是_____.
来源:2012届北京市西城区高三4月第一次模拟考试文科数学
某校高一年级开设研究性学习课程,( )班和(
)班和( )班报名参加的人数分别是
)班报名参加的人数分别是 和
和 .现用分层抽样的方法,从中抽取若干名学生组成研究性学习小组,已知从(
.现用分层抽样的方法,从中抽取若干名学生组成研究性学习小组,已知从( )班抽取了
)班抽取了 名同学.
名同学.
(Ⅰ)求研究性学习小组的人数;
(Ⅱ)规划在研究性学习的中、后期各安排 次交流活动,每次随机抽取小组中
次交流活动,每次随机抽取小组中 名同学发言.求
名同学发言.求 次发言的学生恰好来自不同班级的概率.
次发言的学生恰好来自不同班级的概率.
来源:2012届北京市西城区高三4月第一次模拟考试文科数学
如图,矩形 中,
中,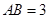 ,
,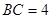 .
.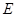 ,
,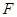 分别在线段
分别在线段 和
和 上,
上, ∥
∥ ,将矩形
,将矩形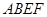 沿
沿 折起.记折起后的矩形为
折起.记折起后的矩形为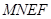 ,且平面
,且平面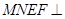 平面
平面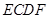 .
.
(Ⅰ)求证: ∥平面
∥平面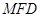 ;
;
(Ⅱ)若 ,求证:
,求证: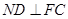 ;
;
(Ⅲ)求四面体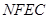 体积的最大值.
体积的最大值.

来源:2012届北京市西城区高三4月第一次模拟考试文科数学
已知椭圆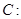
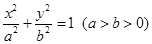 的离心率为
的离心率为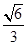 ,一个焦点为
,一个焦点为 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设直线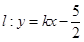 交椭圆
交椭圆 于
于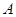 ,
,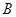 两点,若点
两点,若点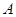 ,
,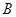 都在以点
都在以点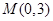 为圆心的圆上,求
为圆心的圆上,求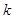 的值.
的值.
来源:2012届北京市西城区高三4月第一次模拟考试文科数学
如图,抛物线 与
与 轴交于两点
轴交于两点 ,点
,点 在抛物线上(点
在抛物线上(点 在第一象限),
在第一象限), ∥
∥ .记
.记 ,梯形
,梯形 面积为
面积为 .
.
(Ⅰ)求面积 以
以 为自变量的函数式;
为自变量的函数式;
(Ⅱ)若 ,其中
,其中 为常数,且
为常数,且 ,求
,求 的最大值.
的最大值.
来源:2012届北京市西城区高三4月第一次模拟考试文科数学
 ,
, ,那么
,那么 ( )
( )



 ,则输出
,则输出 的值为( )
的值为( )




 ,
, ,
, ,则下列结论正确的是( )
,则下列结论正确的是( )



 则|x-3y|的最大值为( )
则|x-3y|的最大值为( )



 ,其中
,其中
 ,且
,且 .则
.则 中所有元素之和是( )
中所有元素之和是( )



 ,
, .若
.若 ,则实数
,则实数 _____.
_____. 的最小正周期为_____.
的最小正周期为_____. 的圆心到直线
的圆心到直线 的距离是_____.
的距离是_____. 则
则 的零点是_____;
的零点是_____; 中,已知
中,已知 .
. ;
; ,△
,△ ,求
,求 .
. ,定义“
,定义“ 变换”:
变换”: 变换成数列
变换成数列 ,其中
,其中 ,且
,且 .这种“
.这种“ .继续对数列
.继续对数列 进行“
进行“ ,依此类推,当得到的数列各项均为
,依此类推,当得到的数列各项均为 时变换结束.
时变换结束. 经过不断的“
经过不断的“ ,
, ,且
,且 .
. ,
, ;
; 次“
次“ 粤公网安备 44130202000953号
粤公网安备 44130202000953号