[安徽]2012届安徽省安庆市高三第二次模拟考试理科数学试卷

复数的共轭复数是a+bi（a,bR）,i是虚数单位，则ab的值是

在同一坐标系下，下列曲线中，右焦点与抛物线y²＝4x的焦点重合的是

A．

B．

C．

D．

设f（x）是定义在R上的偶函数，当x≤0时，f(x)＝log₂(2-x)²，则f（2）＝

以平面直角坐标系的原点为极点，以x轴的正半轴为极轴，建立极坐标系，则曲线（为参数，）上的点到曲线的最短距离是

A．0

B．2－

C．1

D．2

下列命题中错误的是

A．命题“若x2-5x+6=0，则x＝2”的逆否命题是“若x≠2，则x2-5x+6≠0”

B．若x,yR，则“x=y”是成立的充要条件

C．已知命题p和q，若q为假命题，则例题p与q中必一真一假

D．对命题p：，使得x2＋x+1＜0，则则x2＋x+1≥0

已知集合{b}={x∈R|ax²-4x+1=0, a,bR }则a+b＝

A．0或1

B．

C．

D．或

一空间几何体的三视图如图所示（正、侧视图是两全等图形，俯视图是圆及圆的内接正方形），则该几何体的表面积是

A．7cm2

B．（5＋4）cm2

C．（5＋2）cm27

D．（6＋2－2）cm2

函数f(x)的图象如右图所示，已知函数F（x）满足＝f（x），则F（x）的函数图象可能是

已知函数f（x）由下表定义

A．

B．2

C．4

D．5

在△ABC中，a,b,c分别为∠A，∠B，∠C所对应三角形的边长，若，则cosB＝

A．

B．

C．

D．

已知x,y取值如下表：

从散点图中可以看出y与x线性相关，且回归方程为＝0.95x+a，则a＝＿＿＿

已知实数，x，y满足约束条件，则z＝2x＋y的最小值是＿＿＿＿

如图所示，程序框图的输出结果n是＿＿＿＿

设的展开式的各项系数之和为M，二项式系数之和为N，若M，8，N三数成等比数列，则展开式中第四项为＿＿＿＿

如图正方形BCDE的边长为a，已知AB＝BC，将直角△ABE沿BE边折起，A点在面BCDE上的射影为D点，则翻折后的几何体中有如下描述：
（1）ADE所成角的正切值是；
（2）的体积是；
（3）AB∥CD；
（4）平面EAB⊥平面ADEB；
（5）直线BA与平面ADE所成角的正弦值为。
其中正确的叙述有＿＿＿＿＿（写出所有正确结论的编号）。

在△ABC中，，。
（I）求sinC的值；
（II）设BC＝5，求△ABC的面积。

已知数列{a_n}的各项均为正数，其前n项和为S_n，且－1，，数列，，……，是首项为1，公比为的等比数列。
（I）求证：数列{a_n}是等差数列；
（II）若，求数列{c_n}的前n项和Tn。

第11届全国人大五次会议于2012年3月5日至3月14日在北京召开，为了搞好对外宣传工作，会务组选聘了16名男记者和14名记者担任对外翻译工作，调查发现，男、女记者中分别有10人和6人会俄语。
（I）根据以上数据完成以下2X2列联表：

并回答能否在犯错的概率不超过0.10的前提下认为性别与会俄语有关？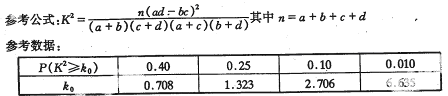

（II）若从会俄语的记者中随机抽取3人成立一个小组，则小组中既有男又有女的概率是多少？
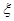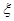（III）若从14名女记者中随机抽取2人担任翻译工作，记会俄语的人数为，求的期望。

如图所示，多面体FE－ABCD中，ABCD和ACFE都是直角梯形，DC∥AB，AE∥CF，平面ACFE⊥平面ABCD，AD＝DC＝CF＝2AE＝，∠ACF＝∠ADC＝。
（I）求证：BC⊥平面ACFE；
（II）求二面角B－FE－D的平面角的余弦值。

已知直线，圆O：＝36（O为坐标原点），椭圆C：＝1（a＞b＞0）的离心率为e＝，直线l被圆O截得的弦长与椭圆的长轴长相等。
（I）求椭圆C的方程；（II）过点（3,0）作直线l，与椭圆C交于A，B两点设（O是坐标原点），是否存在这样的直线l，使四边形为ASB的对角线长相等？若存在　，求出直线l的方程，若不存在，说明理由。

已知函数。
（I）求f(x)的单调区间；
（II）若对任意x∈［1，e］，使得g(x)≥－x²＋（a＋2）x恒成立，求实数a的取值范围；
（III）设F（x）＝，曲线y＝F（x）上是否总存在两点P，Q，使得△POQ是以O（O为坐标原点）为钝角柄点的钝角三角开，且最长边的中点在y轴上？请说明理由。