已知直线
，圆O：
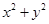＝36（O为坐标原点），椭圆C：
＝1（a＞b＞0）的离心率为e＝
，直线l被圆O截得的弦长与椭圆的长轴长相等。
（I）求椭圆C的方程；（II）过点（3,0）作直线l，与椭圆C交于A，B两点设
（O是坐标原点），是否存在这样的直线l，使四边形为ASB的对角线长相等？若存在 ，求出直线l的方程，若不存在，说明理由。
相关试题
的切线
,交椭圆G于A，B两点.
表示为m的函数，并求
中，
⊥平面
,
，
与底面
， 
.
∥平面
，求
的值；
等于何值时，二面角
的大小为45°？
中，角
所对的
边为
，已知
。
的值；
，且
，求
}中，
，并且对任意
都有
成立，令
．
}的通项公式；（Ⅱ）求数列{
}的前n项和
，不等式
恒成立，求实数
的取值范围；
，满足不等式
，求实数推荐套卷
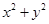已知直线，圆O：＝36（O为坐标原点），椭圆C：＝1（a＞b＞0）的离心率为e＝，直线l被圆O截得的弦长与椭圆的长轴长相等。
（I）求椭圆C的方程；（II）过点（3,0）作直线l，与椭圆C交于A，B两点设（O是坐标原点），是否存在这样的直线l，使四边形为ASB的对角线长相等？若存在 ，求出直线l的方程，若不存在，说明理由。
粤公网安备 44130202000953号