[河南]2012届河南省焦作市高三第一次质量检测理科数学试卷
下列函数中,既是奇函数,又是增函数是( )
| A.f(x)=x|x| | B.f(x)= -x3 |
C.f(x)= |
D.f(x)=  |
如图甲,在透明塑料制成的长方体ABCD—A1B1C1D1容器内灌进一些水,固定容器底面一边BC于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个说法:
①水的部分始终呈棱柱状; ②水面四边形EFGH的面积不改变;
③棱A1D1始终与水面EFGH平行; ④当容器倾斜如图乙时,BE·BF是定值
其中正确说法是 ( )
| A.①②③ | B.①③ | C.①②③④ | D.①③④ |
已知点P是双曲线 右支上一点,
右支上一点, ,分别是双曲线的左、右焦点,I为
,分别是双曲线的左、右焦点,I为 的内心,若
的内心,若  成立,则双曲线的离心率为( )
成立,则双曲线的离心率为( )
| A.4 | B. |
C.2 | D. |
在公比为 的等比数列
的等比数列 中,
中, 与
与 的等差中项是
的等差中项是 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)若函数 ,
, ,的一部分图像如图所示,
,的一部分图像如图所示, ,
, 为图像上的两点,设
为图像上的两点,设 ,其中
,其中 与坐标原点
与坐标原点 重合,
重合, ,求
,求 的值.
的值.
甲、乙两位学生参加数学竞赛培训.现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次.记录如下:
甲:82 81 79 78 95 88 93 84
乙:92 95 80 75 83 80 90 85
(1)画出甲、乙两位学生成绩的茎叶图,指出学生乙成绩的中位数;
(2)现要从中选派一人参加数学竞赛,从平均状况和方差的角度考虑,你认为派哪位学生参加合适?请说明理由;
(3)若将频率视为概率,对学生甲在今后的三次数学竞赛成绩进行预测,记这三次成绩中高于80分的次数为 ,求
,求 的分布列及数学期望
的分布列及数学期望 .
.
如图,矩形ABCD中,AB=CD=2 ,BC=AD=
,BC=AD= 。现沿着其对角线AC将D点向上翻折,使得二面角D—AC—B为直二面角。
。现沿着其对角线AC将D点向上翻折,使得二面角D—AC—B为直二面角。
(Ⅰ)求二面角A—BD—C平面角的余弦值。
(Ⅱ)求四面体ABCD外接球的体积; 
已知椭圆的离心率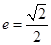 ,左、右焦点分别为
,左、右焦点分别为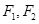 ,定点P
,定点P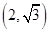 ,点
,点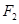 在线段
在线段 的中垂线上.
的中垂线上.
(1)求椭圆C的方程;
(2)设直线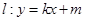 与椭圆C交于M、N两点,直线
与椭圆C交于M、N两点,直线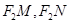 的倾斜角分别为
的倾斜角分别为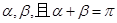 ,求证:直线
,求证:直线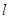 过定点,并求该定点的坐标.
过定点,并求该定点的坐标.
已知函数 .
.
(I)求 在
在 上的最大值;
上的最大值;
(II)若对任意的实数 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(III)若关于 的方程
的方程 在
在 上恰有两个不同的实根,求实数
上恰有两个不同的实根,求实数 的取值范围.
的取值范围.
在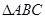 中,AB=AC,过点A的直线与其外接圆交 于点P,交BC延长线于点D。
中,AB=AC,过点A的直线与其外接圆交 于点P,交BC延长线于点D。
(1)求证: 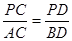 ;
;
(2)若AC=3,求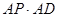 的值。
的值。
在平面直角坐标系xOy中,已知曲线C的参数方程为 .以直角坐标系原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
.以直角坐标系原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为 .点P为曲线C上的一个动点,求点P到直线l距离的最小值
.点P为曲线C上的一个动点,求点P到直线l距离的最小值
 ,则
,则 的共轭复数是 ( )
的共轭复数是 ( )



 )9的展开式的第8项是( )
)9的展开式的第8项是( )


 中,若
中,若 ,则
,则 且
且 ,若数列
,若数列 的前
的前 项和为
项和为 ,且
,且 ∥
∥ ,则
,则 =( )
=( )








 ,直线
,直线 所围成的图形的面积为( )
所围成的图形的面积为( )



 的通项公式为
的通项公式为 ,那么满足
,那么满足 的整
的整 ( )
( ) ,若
,若 ,则
,则 的最小值为( )
的最小值为( ) 上的奇函数
上的奇函数 ,当
,当 时,
时, ,则关于
,则关于 的函数
的函数 的所有零点之和为( )
的所有零点之和为( )



 成立的必要不充分条件 .
成立的必要不充分条件 . 的一条渐近线方程是
的一条渐近线方程是 ,它的一个焦点与抛物线
,它的一个焦点与抛物线 的焦点相同.则双曲线的方程为 .
的焦点相同.则双曲线的方程为 .
 ,不等式
,不等式 恒成立,则实数
恒成立,则实数 的取值范围__________.
的取值范围__________.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号