[北京]2011-2012年北京东城区九年级第一学期期末考试数学卷
如图,在△ABC中,若DE∥BC,AD=5,BD=10,DE=4,则BC的值为
| A.8 | B.9 | C.10 | D.12 |
下列事件 中,属于必然事件的是
中,属于必然事件的是
| A.随机抛一枚硬币,落地后国徽的一面一定朝上 |
| B.打开电视任选一频道,正在播放北京新闻 |
| C.一个袋中只装有5个黑球,从中摸出一个球是黑球 |
| D.某种彩票的中奖率是10%,则购买该种彩票100张一定中奖 |
如图,若AB是⊙O的直径,CD是⊙O的弦,∠ABD=58°, 则∠C的 度数为
| A.116° | B.58° | C.42° | D.32° |
已知x=1是方程x2+bx +b -3=0的一个根,那么此方程的另一个根为
| A.-2 | B.-1 | C.1 | D.2 |
如图,直径AB为6的半圆O,绕A点逆时针旋转60°,此时点B 到了点 ,则图中阴影部分的面积为
,则图中阴影部分的面积为
| A.6π | B.5π | C.4π | D.3π |
如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,直角∠MON的顶点O在AB上, OM、ON分别交CA、CB于点P、Q,∠MON绕点O任意旋转.当 时,
时,  的值为 ;当
的值为 ;当 时,
时, 的值为 .(用含n的式子表示)
的值为 .(用含n的式子表示)
如图,在△ABC中,点D在边AB上,满足且∠ACD =∠ABC,若AC = 2,AD =1,求DB 的长.
的长.
在平面直角坐标系xoy中,已知 三个顶点的坐标分别为
三个顶点的坐标分别为 
⑴ 画出
 ;
;⑵ 画出
 绕点
绕点 顺时针旋转
顺时针旋转 后得到的
后得到的 ,并求出
,并求出 的长.
的长.
已知二次函数y=x2+bx+c中,函数y与自变量x的部分对应值如下表:
| x |
… |
-1 |
0 |
1 |
2 |
3 |
4 |
… |
| y |
… |
8 |
3 |
0 |
-1 |
0 |
3 |
… |
(1) 求该二次函数的解析式;
(2) 当x为何值时,y有最小值,最小值是多少?
(3)
 若A(m,y1),B(m+2, y2)两点都在该函数的图象上,计算当m取何值时,
若A(m,y1),B(m+2, y2)两点都在该函数的图象上,计算当m取何值时,
为了测量校园水平地面上一棵树的高度,数学兴趣小组利用一根标杆、皮尺,设计如图所示的测量方案.已知测量同学眼睛A、标杆顶端F、树的顶端E在同一直线上,此同学眼睛距地面1.6米,标杆为3.1米,且BC=1米,CD=5米,请你根据所给出的数据求树高ED.
如图,邻边不等的矩形花圃ABCD,它的一边AD利用已有的围墙,另外三边所围的栅栏的总长度是6m.若矩形的面积为4m2,请你计算AB的长度(可利用的围墙长度超过6m).
如图,已知直线 交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作
交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作 ,垂足为D.
,垂足为D.(1) 求证:CD为⊙O的切线;
(2) 若CD=2AD,⊙O的直径为10,求线段AC的长.

在一个不透明的口袋里,装有红、白、黄三种颜色的乒乓球(除颜色外其余都相同),其中有白球2个,黄球1个.若从中任意摸出一个球,这个球是白球的概率为0.5 .(1)求口袋中红球的个数;
(2)若摸到红球记0分,摸到白球记1分,摸到黄球记2分,甲从口袋中摸出一个球不放回,再摸出一个.请用画树状图的方法求甲摸到两个球且得2分的概率.
李经理在某地以10元/千克的批发价收购了2 000千克核桃,并借一仓库储存.在存放过程中,平均每天有6千克的核桃损耗掉,而且仓库允许存 放时间最多为60天.若核桃的市场价格在批发价的基础上每天每千克上涨0.5元。
放时间最多为60天.若核桃的市场价格在批发价的基础上每天每千克上涨0.5元。(1)存放x天后,将这批核桃一次性出售,如果这批核桃的销售总金额为y元,试求出y与x之间的函数关系式;
(2)如果仓库存放这批核桃每天需要支出各种费用合计340元,李经理要想获得利润22 500元,需将这批核桃存放多少天后出售?(利润=销售总金额-收购成本-各种费用)
已知:关于 的方程
的方程
 .
.当a取何值时,方程
 有两个不相等的实数根;
有两个不相等的实数根;(2) 当整数a取何值时,方程

 的根都是正整数.
的根都是正整数.
已知△ABC和△ADE是等腰直角三角形,∠ACB=∠ADE=90°,点F为BE中点,连结DF、CF. (1)如图1, 当点D在AB上,点E在AC上,请直接写出此时线段DF、CF的数量关系和位置关系(不用证明);
(2)如图2,在(1)的条件下将△ADE绕点A顺时针旋转45°时,请你判断此时(1)中的结论是否仍然成立,并证明你的判断;
(3)如图3,在(1)的条件下将△ADE绕点A顺时针旋转90°时,若AD=1,AC=
 ,求此时线段CF的长(直接写出结果).
,求此时线段CF的长(直接写出结果).
 的顶点坐标是
的顶点坐标是 
 的图象如图所示,那么一次函数
的图象如图所示,那么一次函数 与反比例函数
与反比例函数 在同一坐标系内的图象大致为
在同一坐标系内的图象大致为 
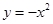 向左平移2个单位,再向上平移1个单位后,得到的抛物线的解析式为 .
向左平移2个单位,再向上平移1个单位后,得到的抛物线的解析式为 .
 ,半径为10,圆心
,半径为10,圆心 .
.
 与x轴交于A、B两点(点A
与x轴交于A、B两点(点A 相似?若存在,请求出点F的坐标,若不存在,请说明理由;
相似?若存在,请求出点F的坐标,若不存在,请说明理由;  ?若存在,求出点G的坐标;若不存在,请说明理由.
?若存在,求出点G的坐标;若不存在,请说明理由. 粤公网安备 44130202000953号
粤公网安备 44130202000953号