李经理在某地以10元/千克的批发价收购了2 000千克核桃,并借一仓库储存.在存放过程中,平均每天有6千克的核桃损耗掉,而且仓库允许存 放时间最多为60天.若核桃的市场价格在批发价的基础上每天每千克上涨0.5元。
放时间最多为60天.若核桃的市场价格在批发价的基础上每天每千克上涨0.5元。(1)存放x天后,将这批核桃一次性出售,如果这批核桃的销售总金额为y元,试求出y与x之间的函数关系式;
(2)如果仓库存放这批核桃每天需要支出各种费用合计340元,李经理要想获得利润22 500元,需将这批核桃存放多少天后出售?(利润=销售总金额-收购成本-各种费用)
相关知识点
推荐套卷
 (2)
(2)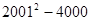

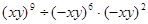

 +
+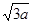 )(
)(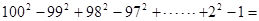 。
。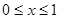 ,若
,若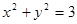 ,
, 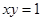 ,则
,则
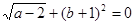 ,则
,则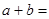 ________
________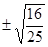 =,
=,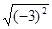 =.
=. 粤公网安备 44130202000953号
粤公网安备 44130202000953号