某地区有城区居民和农村居民共80万人.某机构准备采用抽取样本的方法调查该地区居民“获取信息的最主要途径”.
(1)该机构设计了以下三种调查方案:
方案一:随机抽取部分城区居民进行调查;
方案二:随机抽取部分农村居民进行调查;
方案三:随机抽取部分城区居民和部分农村居民进行调查.
其中最具有代表性的一个方案是 ;
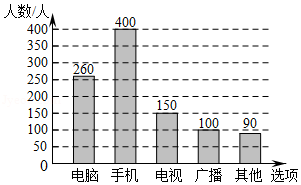
(2)该机构采用了最具有代表性的调查方案进行调查.供选择的选项有:电脑、手机、电视、广播、其他,共五个选项.每位被调查居民只选择一个选项.现根据调查结果绘制如下统计图,请根据统计图回答下列问题:
①这次接受调查的居民人数为 人;
②统计图中人数最多的选项为 ;
③请你估计该地区居民和农村居民将“电脑和手机”作为“获取信息的最主要途径”的总人数.