[河南]2012届河南省南阳市高三上学期期终质量评估理科数学
设m、n是两条不同的直线,α、β是两个不同的平面.考察下列命题,其中真命题是
A.m⊥α,n β,m⊥n β,m⊥n α⊥β α⊥β |
B.α∥β,m⊥α,n∥β m⊥n m⊥n |
C.α⊥β,m⊥α,n∥β m⊥n m⊥n |
D.α⊥β,α∩β=m,m⊥n n⊥β n⊥β |
已知命题p: ∈R,使得a
∈R,使得a +2x+1<0成立,当
+2x+1<0成立,当 为假命题时,实数a的取值范围是
为假命题时,实数a的取值范围是
| A.[1,+∞) | B.(-∞,1] | C.[0,1) | D.(-∞,1) |
设函数f(x)=sin(2x+ ),则下列结论正确的是
),则下列结论正确的是
A.f(x)的图像关于直线x= 对称 对称 |
B.f(x)的图像关于点( ,0)对称 ,0)对称 |
C.f(x)的最小正周期为π,且在[0, ]上为增函数 ]上为增函数 |
D.把f(x)的图像向左平移 个单位,得到一个偶函数的图像 个单位,得到一个偶函数的图像 |
圆2 +2
+2 =1与直线xsinθ+y-1=0(θ≠
=1与直线xsinθ+y-1=0(θ≠ +kπ,k∈Z)的位置关系是
+kπ,k∈Z)的位置关系是
| A.相切 | B.相离 |
| C.相交 | D.不能确定 |
设函数f(x)是定义在R上的奇函数,当x≥0时,f(x)单调递减,若数列{ }是等差数列,且a3<0,则f(a1)+f(a2)+f(a3)+f(a4)+f(a5)的值
}是等差数列,且a3<0,则f(a1)+f(a2)+f(a3)+f(a4)+f(a5)的值
| A.恒为正数 | B.恒为负数 | C.恒为0 | D.可正可负 |
点M(a,b)在由不等式组 确定的平面区域内,则点N(a+b,a-b)所在平面区域的面积是
确定的平面区域内,则点N(a+b,a-b)所在平面区域的面积是
| A.1 | B.2 | C.4 | D.8 |
已知P是双曲线 (a>0,b>0)上的点,F1,F2是其焦点,双曲线的离心率是
(a>0,b>0)上的点,F1,F2是其焦点,双曲线的离心率是 ,且
,且 ·
· =0,若△PF1F2的面积为9,则a+b的值为
=0,若△PF1F2的面积为9,则a+b的值为
| A.5 | B.6 | C.7 | D.8 |
.已知球O为棱长为1的正方体ABCD-A1B1C1D1的内切球,则平面ACD1截球O的截面面积为
A. π π |
B. |
C. π π |
D. |
已知f(x)=ln( +1),g(x)=
+1),g(x)= -m,若
-m,若 ∈[0,3],
∈[0,3], ∈[1,2],使得f(x1)>g(x2),则实数m的取值范围是
∈[1,2],使得f(x1)>g(x2),则实数m的取值范围是
A.[ ,+∞) ,+∞) |
B.(-∞, ] ] |
C.[ ,+∞) ,+∞) |
D.(-∞,- ] ] |
已知点G是△ABC的重心, =λ
=λ +μ
+μ (λ,μ∈R),若∠A=120°,
(λ,μ∈R),若∠A=120°, ·
· =-2,则|
=-2,则| |的最小值是_____________.
|的最小值是_____________.
已知集合U={x| >-2且x∈Z},集合A={x|ax-1=0},集合B={x|
>-2且x∈Z},集合A={x|ax-1=0},集合B={x| -(a+3)x+2a+2=0),若CUA=B,求a的值.
-(a+3)x+2a+2=0),若CUA=B,求a的值.
已知△ABC的三个内角A、B、C所对的边分别为a,b, c,向量m=(1,1- sinA),n=(cosA,1),且m⊥n.
sinA),n=(cosA,1),且m⊥n.
(Ⅰ)求角A;
(Ⅱ)若b+c= a,求sin(B+
a,求sin(B+ )的值.
)的值.
数列{ }的前n项和记为
}的前n项和记为 ,a1=t,
,a1=t, =2
=2 +1(n∈N+).
+1(n∈N+).
(Ⅰ)当t为何值时,数列{ }是等比数列;
}是等比数列;
(Ⅱ)在(Ⅰ)的条件下,若等差数列{ }的前n项和
}的前n项和 有最大值,且
有最大值,且 =15,又
=15,又
a1+b1,a2+b2,a3+b3成等比数列,求 .
.
如图,四棱锥P-ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.
(Ⅰ)证明PA∥平面BDE;
(Ⅱ)求二面角B-DE-C的余弦值;
(Ⅲ)在棱PB上是否存在点F,使PB⊥平面DEF.证明你的结论.
如图,已知过点D(0,-2)作抛物线C1: =2py(p>0)的切线l,切点A在第二象限.
=2py(p>0)的切线l,切点A在第二象限.
(Ⅰ)求点A的纵坐标;
(Ⅱ)若离心率为 的椭圆
的椭圆 (a>b>0)恰好经过点A,设直线l交椭圆的另一点为B,记直线l,OA,OB的斜率分别为k,k1,k2,若k1+2k2=4k,求椭圆方程.
(a>b>0)恰好经过点A,设直线l交椭圆的另一点为B,记直线l,OA,OB的斜率分别为k,k1,k2,若k1+2k2=4k,求椭圆方程.
 的共轭复数为
的共轭复数为 -
-
 是等差数列{
是等差数列{ }的前n项和,S5=3(a2+a8),则
}的前n项和,S5=3(a2+a8),则 的值为
的值为






 =_______________.
=_______________. ,则tanθ=______________.
,则tanθ=______________. 若f(a)>f(-a),则实数a的取值范围是__________.
若f(a)>f(-a),则实数a的取值范围是__________.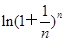 <1.
<1. 粤公网安备 44130202000953号
粤公网安备 44130202000953号