[湖北]2012届湖北省黄冈市高三上学期期末考试理科数学
下列四种说法中,错误的个数是( )
①A={0,1)的子集有3个;
②“若am2 <bm2,则a<b”的逆命题为真;
③“命题p q为真”是“命题p
q为真”是“命题p q为真”的必要不充分条件;
q为真”的必要不充分条件;
④命题“ ∈R,均有
∈R,均有 ≥0”的否定是:“
≥0”的否定是:“ ∈R,使得x2—3x-2≤0”
∈R,使得x2—3x-2≤0”
| A.0个 | B.1个 | C.2个 | D.3个 |
设 是奇函数,则使
是奇函数,则使 的x的取值范围是( )
的x的取值范围是( )
| A.(—1,0) | B.(0,1) |
| C.(一∞,0) | D.(一∞,0) (1,+∞) (1,+∞) |
用0,1,2,3,4排成无重复字的五位数,要求偶数字相邻,奇数字也相邻,则这样的五位数的个数是( )
| A.36 | B.32 | C.24 | D.20 |
函数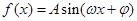 (其中
(其中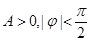 )的图象如图所示,为了得到
)的图象如图所示,为了得到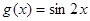 的图像,则只要将
的图像,则只要将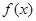 的图像 ( )
的图像 ( )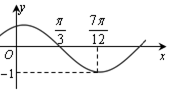
A.向右平移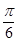 个长度单位 个长度单位 |
B.向右平移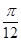 个长度单位 个长度单位 |
C.向左平移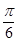 个长度单位 个长度单位 |
D.向左平移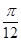 个长度单位 个长度单位 |
设x,y满足约束条件 ,若目标函数
,若目标函数 的最大值为8,则a+b的最小值为( )
的最大值为8,则a+b的最小值为( )
| A.2 | B.4 | C.6 | D.8 |
设数列 为等差数列,其前n项的和为Sn,已知
为等差数列,其前n项的和为Sn,已知 ,若对任意
,若对任意 都有Sn≤Sk成立,则k的值为( )
都有Sn≤Sk成立,则k的值为( )
| A.22 | B.21 | C.20 | D.19 |
过双曲线 的左焦点F(一c,0)(c>o),作圆:
的左焦点F(一c,0)(c>o),作圆: 的切线,切点为E,延长FE交双曲线右支于点P,若
的切线,切点为E,延长FE交双曲线右支于点P,若 ,则双曲线的离心率为( )
,则双曲线的离心率为( )
A. |
B. |
C. |
D. |
(1)(参数方程)在极坐标系中,定点A(2, ),动点B在直线
),动点B在直线 =
= 上运动,则线段AB的最短长度为 .
上运动,则线段AB的最短长度为 .
(2)(几何证明选讲)如图,在半径为2的⊙O中,∠AOB=90°,D为OB的中点,AD的延长线交⊙O于点E,则线段DE的长为 。
如图,设D是图中边长为4的正方形区域,E是D内函数y= 图象下方的点构成的阴影区域.向D中随机投一点,则该点落入中E的概率为 。
图象下方的点构成的阴影区域.向D中随机投一点,则该点落入中E的概率为 。
本小题满分12分)设函数
(1)求函数 取最值时x的取值集合;
取最值时x的取值集合;
(2)在△ABC中,角A、B、C的对边分别是a,b,c,且满 求函数
求函数 的取值范围.
的取值范围.
已知函数 的图像经过(o,1),且
的图像经过(o,1),且
(1)求 的值域;
的值域;
(2)设命题 ,命题q:函数
,命题q:函数 在R上无极值,是否存在实数m满足复合命题p且q为真命题?若存在,求出m的范围;若不存在,说明理由.
在R上无极值,是否存在实数m满足复合命题p且q为真命题?若存在,求出m的范围;若不存在,说明理由.
(本小题满分12分)某公司为了实现2011年1000万元利润的目标,准备制定一个激励销售人员的奖励方案:销售利润达到10万元时,按销售利润进行奖励,且奖金数额y(单位:万元)随销售利润x(单位:万元)的增加而增加,但奖金数额不超过5万元,同时奖金数额不超过利润昀25%,现有三个奖励模型: ,问其中是否有模型能完全符合公司的要求?说明理由.
,问其中是否有模型能完全符合公司的要求?说明理由.
(参考数据: )
)
(本小题满分12分)已知数列 是首项为
是首项为 ,公比
,公比 的等比数列.设
的等比数列.设 ,数列
,数列 满足
满足 以.
以.
(1)求证:数列 成等差数列;
成等差数列;
(2)求数列 的前n项和
的前n项和
(3)若
 对一切正整数n恒成立,求实数m的取值范围.
对一切正整数n恒成立,求实数m的取值范围.
本小题满分13分)已知圆 ,定点A(2,0),M为圆C上一动点,点P在AM上,点N在C、M上(C为圆心),且满足
,定点A(2,0),M为圆C上一动点,点P在AM上,点N在C、M上(C为圆心),且满足 ,设点N的轨迹为曲线E.
,设点N的轨迹为曲线E.
(1)求曲线E的方程;
(2)过点B(m,0)作倾斜角为 的直线
的直线 交曲线E于C、D两点.若点Q(1,0)恰在以线段CD为直径的圆的内部,求实数m的取值范围.
交曲线E于C、D两点.若点Q(1,0)恰在以线段CD为直径的圆的内部,求实数m的取值范围.
 则A
则A B等于( )
B等于( )
 )
)

 ,则函数f(x)在其定义域内的零点个数是( )
,则函数f(x)在其定义域内的零点个数是( ) 则
则 = 。
= 。 上三点,且
上三点,且 = .
= . ,展开式中含
,展开式中含 项的系数是 。
项的系数是 。

 的单调递增区间;
的单调递增区间; 的图象为曲线C.设点A(x1,y1),B(x2,y2)是曲线C上的不同两点.如果在曲线C上存在点M(x0,y0),使得:①
的图象为曲线C.设点A(x1,y1),B(x2,y2)是曲线C上的不同两点.如果在曲线C上存在点M(x0,y0),使得:① ;②曲线C在点M处的切线平行于直线AB,则称函数F(x)夺在“中值相依切线”,
;②曲线C在点M处的切线平行于直线AB,则称函数F(x)夺在“中值相依切线”, 粤公网安备 44130202000953号
粤公网安备 44130202000953号