[北京]2011-2012学年北京市石景山区九年级上学期期末考试数学卷
如图,在Rt△ABC中,∠C=90°,BC=3,AC=2, 则tanB的值是
A. |
B. |
C. |
D. |
如图,⊙O的弦AB=8,OE⊥AB于点E,且OE=3,则⊙O的半径是 
A. |
B.2 | C.10 | D.5 |
对于反比例函数 ,下列说法正确的是
,下列说法正确的是
| A.图象经过点(2,-1) | B.图象位于第二、四象限 |
| C.图象是中心对称图形 | D.当x<0时,y随x的增大而增大 |
一枚质地均匀的正方体骰子,其六个面上分别刻有1、2、3、4、5、6六个数字,投掷这个骰子一次,则向上一面的数字大于4的概率是
A. |
B. |
C. |
D. |
在平面直角坐标系中,将二次函数 的图象向上平移2个单位,所得图象的解析式为
的图象向上平移2个单位,所得图象的解析式为
A. |
B. |
C. |
D. |
.如图,在△ABC中,DE∥BC,AD=2,AB=6,AE=3,则CE的长为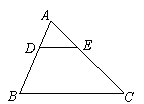
| A.9 | B.6 | C.3 | D.4 |
如图,若AD是⊙ 的直径,AB是⊙O的弦,∠DAB=50°,点C在圆上,则
的直径,AB是⊙O的弦,∠DAB=50°,点C在圆上,则
∠ACB的度数是
| A.100° | B.50° | C.40° | D.20° |
如图,动点P从点A出发,沿线段AB运动至点B.点P在运动过程中速度大小不变.则以点A为圆心,线段AP长为半径的圆的面积S与点P的运动时间t之间的函数图象大致是
如图,是河堤的横断面,堤高BC=5米,迎水坡AB的坡比1: (坡比是坡面的铅直高度BC与水平宽度AC之比),则AC的长是 米.
(坡比是坡面的铅直高度BC与水平宽度AC之比),则AC的长是 米.
已知抛物线 (
( >0)过O(0,0)、A(
>0)过O(0,0)、A( ,0)、B(
,0)、B( ,
, )、C(4,
)、C(4, )四点,则
)四点,则
 (填“>”、“<”或“=”).
(填“>”、“<”或“=”).
如图,有一边长为4的等边三角形纸片,要从中剪出三个面积相等的扇形,那么剪下的其中一个扇形ADE(阴影部分)的面积为 ;若用剪下的一个扇形围成一个圆锥,该圆锥的底面圆的半径r是 .
如图,⊙A与x轴交于B(2,0)、 (4,0)两点,OA=3,点P是y轴上的一个动点,PD切⊙O于点D,则PD的最小值是 .
(4,0)两点,OA=3,点P是y轴上的一个动点,PD切⊙O于点D,则PD的最小值是 .
已知:函数 是二次函数.
是二次函数.(1)求m的值;
(2)写出这个二次函数图象的对称轴: ,顶点坐标: ;
(3)求图象与
 轴的交点坐标.
轴的交点坐标.
如图,在△ABC中,CD、BE分别是AB、AC边上的高,∠EBC=45°,BE=6,CD= ,求∠DCB的度数.
,求∠DCB的度数. 
如图,一次函数 的图象与x轴、y轴分别交于点A、点B,与反比例函数
的图象与x轴、y轴分别交于点A、点B,与反比例函数 的图象交于点C,CD⊥x轴于点D,求四边形OBCD的面积.
的图象交于点C,CD⊥x轴于点D,求四边形OBCD的面积.
袋中装有编号为1,2,3的三个质地均匀、大小相同的球,从中随机取出一球记下编号后,放入袋中搅匀,再从袋中随机取出一球,记下编号.将两次编号作为数字求和.(1)请用树状图或列表的方法表示可能出现的所有结果;
(2)求两次所取球的编号之和是偶数的概率.
如图,河两岸a,b互相平行,C,D是河岸a上间隔40米的两根电线杆,某人在河岸b上的A处,测得∠DAE=45°,然后沿河岸走了30米到达B处,测得∠CBE=60°,求河的宽度(结果精确到1米, ).
).
某超市按每袋20元的价格购进某种干果.销售过程中发现,每月销售量y(袋)与销售单价x(元)之间的关系可近似地看作一次函数: (
( ).
).(1)当x=45元时,y= 袋;当y=200袋时,x= 元;
(2)设这种干果每月获得的利润为w(元),当销售单价定为多少元时,每月 可获得最大利润?最大利润是多少?
如图,抛物线与 轴交于A(1,0),B(
轴交于A(1,0),B( ,0)两点,与
,0)两点,与 轴交于点C(0,3).
轴交于点C(0,3).
(1)求此抛物线的解析式;
(2)在x轴上找一点D,使得以点A、C、D为顶点的三角形是直角三角形,求点D的坐标.
如图,在三角形ABC中,以 为直径作⊙O,交AC于点E,OD⊥AC于D,∠AOD=∠C.
为直径作⊙O,交AC于点E,OD⊥AC于D,∠AOD=∠C.
(1)求证:BC为⊙O的切线;
(2)若
 ,求OD的长.
,求OD的长.
如图1,在△ABC中,∠ACB=90°,AC=3,BC=4,将△ABC绕顶点C顺时针旋转30°,得到△A′B′C.联结A′A、B′B,设△ACA′和△BCB′的面积分别为S△ACA′ 和S△BCB′.
(1)直接写出S△ACA′ ︰S△BCB′ 的值 ;
(2)如图2,当旋转角为
 (0°<
(0°< <180°)时,S△ACA′ 与S△BCB′ 的比值是否发生变化,若不变请证明;若改变,写出变化后的比值(可用含
<180°)时,S△ACA′ 与S△BCB′ 的比值是否发生变化,若不变请证明;若改变,写出变化后的比值(可用含 的代数式表示).
的代数式表示).
.已知函数 (m是常数).
(m是常数).(1)求证:不论m为何值,该函数的图象都经过y轴上的一个定点;
(2)若一次函数
 的图象与该函数的图象恰好只有一个交点,求m的值 及这个交点的坐标.
的图象与该函数的图象恰好只有一个交点,求m的值 及这个交点的坐标.
 .
. △ABC中,
△ABC中, ,点
,点 在
在 上,
上, 为⊙
为⊙ 于
于 ,若
,若 ,求⊙
,求⊙
 是矩形
是矩形 绕点B顺时针旋转得到的.其中点
绕点B顺时针旋转得到的.其中点 在
在 轴负半轴上,线段
轴负半轴上,线段 在
在 轴正半轴上,
轴正半轴上, 点的坐标为
点的坐标为 .
.
 的图象经过
的图象经过 两点且图象顶点
两点且图象顶点 的纵坐标为
的纵坐标为 .求这个二次函数的解析式;
.求这个二次函数的解析式; 所在直线的解析式;
所在直线的解析式; ,若存 在,请求出点P的坐标,若不存在,请说明理由.
,若存 在,请求出点P的坐标,若不存在,请说明理由. 粤公网安备 44130202000953号
粤公网安备 44130202000953号