[浙江]2011年上期浙江省温州市十校高三期中联考理科数学试卷
已知全集U=R,集合A={x|-2≤x≤3},B={x|x<-1或x>4},那么集合A∩(?UB)等于
A.{x|-2≤x<4} B.{x|x≤3或x≥4} C.{x|-2≤x<-1} D.{x|-1≤x≤3}
在二项式 的展开式中,各项系数之和为A,各项二项式系数之和为B,
的展开式中,各项系数之和为A,各项二项式系数之和为B,
且 ,则展开式中常数项的值为
,则展开式中常数项的值为
| A.6 | B.9 | C.12 | D.18 |
1号箱中有2个白球和4个红球,2号箱中有5个白球和3个红球,现随机地从1号箱中取出一球放入2号箱,然后从2号箱随机取出一球,则从2号箱取出红球的概率是
A. |
B. |
C.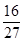 |
D.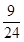 |
命题A: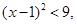 命题B:(x+2)·(x+a)<0;若A是B的充分不必要条件,则a的取值范围是
命题B:(x+2)·(x+a)<0;若A是B的充分不必要条件,则a的取值范围是
| A.(-∞,-4) | B.[4,+∞) | C.(4,+∞) | D.(-∞,-4] |
已知O为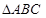 内任意的一点,若对任意
内任意的一点,若对任意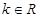 有
有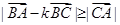 则
则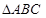 一定是
一定是
| A.直角三角形 | B.钝角三角形 | C.锐角三角形 | D.不能确定 |
函数y=3sin(-2x-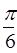 )(x∈[0,π])的单调递增区间是
)(x∈[0,π])的单调递增区间是
A.[0, ] ] |
B.[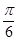 , ,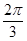 ] ] |
C.[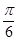 , ,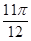 ] ] |
D.[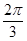 , ,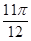 ] ] |
在△ABC中,a,b,c分别为角A,B,C的对边,且cos2B+cosB+cos(A-C)=1,则
A.a,b,c成等差数列 B.a,b,c成等比数列
C.a,c,b成等差数列 D.a,c,b成等比数列
复数z=cos75o+isin75o (i是虚数单位),则在复平面内z2对应的点位于第____象限。
现有一个关于平面图形的命题:如图所示,同一个平面内有两个边长都是 的正方形,其中一个正方形的某个顶点在另一个正方形的中心,则这两个正方形重叠部分的面积恒为
的正方形,其中一个正方形的某个顶点在另一个正方形的中心,则这两个正方形重叠部分的面积恒为 。类比到空间,有两个棱长均为
。类比到空间,有两个棱长均为 的正方体,其中一个正方体的某个顶点在另一
的正方体,其中一个正方体的某个顶点在另一
个正方体的中心,则这两个正方体重叠部分的体积恒为_____▲_ ___。
___。
10双互不相同的鞋子混装在一个袋子中,从中任意取4只,4只鞋子中有两只成双,另两只不成双的取法数为_ ▲ .
已知△ABC中,角A、B、C的对边为a,b,c,向量

 =
= ,且
,且 .
.
(1) 求角C;
(2)若 ,试求
,试求 的值.
的值.
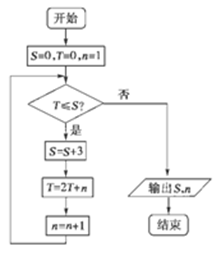
一个均匀的正四面体的四个面上分别涂有1,2,3,4四个数字,现随机投掷两次,正四面体面朝下的数字分别为 ,记
,记 .
.
(1)分别求出 取得最大值和最小值时的概率; (2)
取得最大值和最小值时的概率; (2) 求
求 的分布列及数学期望.
的分布列及数学期望.
如图,抛物线 第一象限部分上的一系列点
第一象限部分上的一系列点 与y正半轴上的点
与y正半轴上的点 及原点,构成一系列正三角形
及原点,构成一系列正三角形 (记
(记 为O),记
为O),记 。
。
(1)求 的值;(2)求数列
的值;(2)求数列 的通项公式
的通项公式 ;
;
(3)求证:

 ,B=
,B=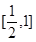 ,函数
,函数 若
若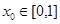 且
且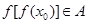 ,则
,则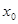 的取值范围为
的取值范围为 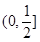



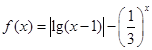 有两个零点x1,x2,则有
有两个零点x1,x2,则有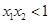
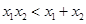
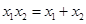

 则
则 ▲
▲  则
则 的最大值是 ▲ 。
的最大值是 ▲ 。 ,
, ,且
,且 ,则
,则 最大值是____▲____。
最大值是____▲____。 ,若
,若 有六个不同的单调区间,
有六个不同的单调区间, 的取值范围为 ▲ .
的取值范围为 ▲ . .若过点
.若过点 可作曲线
可作曲线 的切线有三条,求实数
的切线有三条,求实数 的取值范围.
的取值范围. 时,f
时,f >f
>f ;
; 粤公网安备 44130202000953号
粤公网安备 44130202000953号