[河南]2011届河南省平顶山市第二次中考模拟考试数学试卷
某班数学活动小组5位同学的家庭人口数分别为3、2、4、3、3.设这组数据的平均数为a,中位数为b,则下列各式正确的是( )
| A.a=b<c | B.a<b<c | C.a<b=c | D.a=b=c |
下图是由四个相同的小立方体组成的立体图形的主视图和左视图,那么原立体图形可能是( )
| A.①② | B.②③ | C.①③ | D.①②③ |
如图,已知⊙ 与⊙
与⊙ 关于
关于 轴对称,点
轴对称,点 的坐标为
的坐标为 ,两圆相交于A、B,且
,两圆相交于A、B,且 ,则图中阴影部分的面积是( )
,则图中阴影部分的面积是( )
A.4π– 8 B.8π– 16
C.16π– 16 D.16π– 32
将2个黑球,3个白球,4个红球放入一个不透明的袋子里,从中摸出8个球,恰好红球、白球、黑球都摸到,这个事件是事件 (填“必然”或“不可能”或“随机”).
人的正常体温为37℃,它与在数学大家庭中被称为黄金数的0.618和乘积为 .℃(结果保留三位有效数字).在这一气温下,人体的新陈代谢、生理节奏和生量机能都处于最佳状态.
.如图,⊙0内切于△ABC,切点分别为D、E、F. 已知<B=50°,<C=60°,连结OE、OF、DE、DF.则<EDF= 度.
王英同学从A地沿北偏西60°方向走100米到达B地,再从B地向正南方向走200米到C地,此时王英同学离A地 米.
如图,△ABC是边长为3的等边三角形,△ BDC是等腰三角形,且△BDC=120°,以D为顶点作一个60°角,使其两边分别交AB于M交AC于点N,连接MN,则△AMN的周长为 .
已知,如图,EG∥AF.请你从①DE =" DF" ;②AB =" AC " ③BE = CF中,选择两个作为已知条件,剩余一个作为结 论,写出一个真命题(只需写出一种情况,)并加以证明.
论,写出一个真命题(只需写出一种情况,)并加以证明.
已知:EC∥AF, , ,
求证: .
证明
如图,在平面直角坐标系中,△ABC与△A1B1C1关于点E成中心对称
(1)画出对称中心E,并写出E、A、C的坐标;
(2)P(a,b)是△ABC的边上AC上一点,△ABC经平移后,点P的对应点是P2(A+6,B+2),请画出上述平移后的△A 2B2C2,并判断△A2B2C2与△A1B1C1的位置关系(直接写出结果).
2B2C2,并判断△A2B2C2与△A1B1C1的位置关系(直接写出结果).
某种子培育基地用A、B、C、D、四种型号的小麦种子共2000粒进行发芽实验,从中选出发芽率高的种子进行推广.通过实验得知,C型号种子的发芽率为95%。根据实验数据绘制了图1和图2两幅尚不完整的统计图.(说明:图1表示四种型号种子占总粒数的比例,图2表示四种型号种子的发芽数)
(1)D型号种子粒数是多少?并将图2的统计图补充完整;
(2)通过计算说明,应选哪一个型号的种子推广;
(3)若将所有的 已发芽的种子放在一起,从中随机取出一粒,求取到B型号发芽种子的概率.
已发芽的种子放在一起,从中随机取出一粒,求取到B型号发芽种子的概率.
如图,在平行四边形ABCD中,AB⊥AC,AB=1,BC= ,对角线AC、BD相交于点0,将直线AC绕点0顺时针旋转,分别交BC、AD于点E、F.
,对角线AC、BD相交于点0,将直线AC绕点0顺时针旋转,分别交BC、AD于点E、F.
(1)求证:当旋转角为90°时,四边形ABEF为平形四边形;
(2)在旋转过程中,四边形BEDF可能是菱形吗?如果不能,请说明理由;如果能,说明理由,并求出此时AC绕点0顺时针旋转的度数.
如图,Rt△ABC中,<ACB=90°,AC="4" ,AB="5" ,点P是AC上的动点(P不与A、C重合),设PC=x,点P到AB的距离PQ为y.
(1)求y与x的函数表达式,并写出自变量x的取值范围;
(2)试讨论以P为圆心、半径长为x的圆与AB所在直线的位置关系,并指出相应的x取值范围.
某校原有600张旧课桌急需维修,现有A、B、C三个工程队. A、B队的工作效率相同,且都为C队的2倍,若由一个工程队单独完成,C队比A队要多用10天.学校决定由三个工程队一齐施工,要求最多6天完成维修任务.三个工程队都按原来的工作效率施工2天,学校又清理出需要维修的课桌360张,为了不超过6天时限,工程队决定从第3天开始,各自都提高工作效率,A、B队提高的工作效率仍然都是C队提高的2倍.这样他们至少还需要3天才能完成整个维修任务.
(1)求工程队A原来平均每天维修课桌的张数;
(2)求工程队A提高工作效率后平均每天多维修课桌张数的取值范围.
如图1,已知抛物线经过原点0和x轴上另一个点E,顶点M的坐标是(2,4); 矩形ABCD的顶点A与点0重合,AD、AB分别在x轴和y轴上,且AD="2" ,AB=3.
(1)求该抛物线所参应的函数表达式;
(2)将矩形ABCD以每秒1个单位长度的速度从图1所示的位置沿x轴的正方向匀速平行移动,同时一动点P也以相同的速度从点A出发向B匀速移动,设它们运动的时间为t秒(0≤t≤3),直线AB与该抛物线的交点为N(如图2).
①当t= 时,判断点P时否在直线ME上,并说明理由;
时,判断点P时否在直线ME上,并说明理由;
②设以P、N、C、D为顶点的图形面积为S,试部S是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
 有意义,则x应满足的条件是( )
有意义,则x应满足的条件是( )

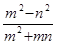 的结果为 .
的结果为 .
 粤公网安备 44130202000953号
粤公网安备 44130202000953号