2022年吉林省长春市中考数学试卷

如图是由5个相同的小正方体组合而成的立体图形，其主视图是（　　）

长春轨道客车股份有限公司制造的新型奥运版复兴号智能动车组，车头采用鹰隼形的设计，能让性能大幅提升，一列该动车组一年运行下来可节省约1800000度电，将数据1800000用科学记数法表示为（　　）

不等式 $x+2＞3$的解集是（　　）

实数 $a，b$在数轴上对应点的位置如图所示，下列结论正确的是（　　）

如图是长春市人民大街下穿隧道工程施工现场的一台起重机的示意图，该起重机的变幅索顶端记为点 $A$，变幅索的底端记为点 $B$， $AD$垂直地面，垂足为点 $D$， $BC\perp AD$，垂足为点 $C$．设 $\angle ABC＝\alpha$，下列关系式正确的是（　　）

如图，四边形 $ABCD$是 $\odot O$的内接四边形，若 $\angle BCD＝121°$，则 $\angle BOD$的度数为（　　）

如图，在△ABC中，根据尺规作图痕迹，下列说法不一定正确的是（　　）

如图，在平面直角坐标系中，点P在反比例函数 $y=\frac{k}{x}$（k＞0，x＞0）的图象上，其纵坐标为2，过点P作PQ∥y轴，交x轴于点Q，将线段QP绕点Q顺时针旋转60°得到线段QM．若点M也在该反比例函数的图象上，则k的值为（　　）

分解因式： $m^2+3m＝$　　 ．

若关于x的方程 $x^2+x+c＝0$有两个相等的实数根，则实数c的值为 　 　．

《算法统宗》是中国古代重要的数学著作，其中记载：我问开店李三公，众客都来到店中，一房七客多七客，一房九客一房空．其大意为：今有若干人住店，若每间住7人，则余下7人无房可住；若每间住9人，则余下一间无人住．设店中共有x间房，可求得x的值为 　 　．

将等腰直角三角板与量角器按如图所示的方式摆放，使三角板的直角顶点与量角器的中心O重合，且两条直角边分别与量角器边缘所在的弧交于A、B两点．若OA＝5厘米，则 $\stackrel{̂}{\mathit{AB}}$的长度为 　 　厘米．（结果保留π）

跳棋是一项传统的智力游戏．如图是一副跳棋棋盘的示意图，它可以看作是由全等的等边三角形ABC和等边三角形DEF组合而成，它们重叠部分的图形为正六边形．若AB＝27厘米，则这个正六边形的周长为 　 　厘米．

已知二次函数 $y＝﹣x^2﹣2x+3$，当 $a\le x\le \frac{1}{2}$时，函数值y的最小值为1，则a的值为 　　．

先化简，再求值： $（2+a）（2﹣a）+a（a+1）$，其中 $a=\sqrt{2}-4$．

抛掷一枚质地均匀的普通硬币，仅有两种可能的结果：“出现正面”或“出现反面”，正面朝上记2分，反面朝上记1分．小明抛掷这枚硬币两次，用画树状图（或列表）的方法，求两次分数之和不大于3的概率．

为了让学生崇尚劳动，尊重劳动，在劳动中提升综合素质，某校定期开展劳动实践活动．甲、乙两班在一次体验挖土豆的活动中，甲班挖1500千克土豆与乙班挖1200千克土豆所用的时间相同．已知甲班平均每小时比乙班多挖100千克土豆，问乙班平均每小时挖多少千克土豆？

图①、图②、图③均是5×5的正方形网格，每个小正方形的边长均为1，其顶点称为格点，△ABC的顶点均在格点上．只用无刻度的直尺，在给定的网格中，按下列要求作图，保留作图痕迹．

（1）网格中△ABC的形状是 　 　；

（2）在图①中确定一点D，连结DB、DC，使△DBC与△ABC全等；

（3）在图②中△ABC的边BC上确定一点E，连结AE，使△ABE∽△CBA；

（4）在图③中△ABC的边AB上确定一点P，在边BC上确定一点Q，连结PQ，使△PBQ∽△ABC，且相似比为1：2．

如图，在Rt△ABC中， $\angle ABC＝90°$， $AB＜BC$．点D是AC的中点，过点D作DE⊥AC交BC于点E．延长ED至点F，使得DF＝DE，连结AE、AF、CF．

（1）求证：四边形AECF是菱形；

（2）若 $\frac{\mathit{BE}}{\mathit{EC}}=\frac{1}{4}$，则 $\tan \angle BCF$的值为 　 　．

党的十八大以来，我国把科技自立自强作为国家发展的战略支撑，科技事业发生了历史性、整体性、格局性变化，成功跨入创新型国家的行列，专利项目多项指数显著攀升．如图是长春市2016年到2020年专利授权情况的统计图．

根据以上信息回答下列问题：

（1）长春市从2016年到2020年，专利授权量最多的是 　 　年；

（2）长春市从2016年到2020年，专利授权量年增长率的中位数是 　 　；

（3）与2019年相比，2020年长春市专利授权量增加了 　 　件，专利授权量年增长率提高了 　 　个百分点；（注：1%为1个百分点）

（4）根据统计图提供的信息，有下列说法，正确的画“√”，错误的画“×”．

①因为2019年的专利授权量年增长率最低，所以2019年的专利授权量的增长量就最小． 　　

②与2018年相比，2019年的专利授权量年增长率虽然下降，但专利授权量仍然上升．这是因为专利授权量年增长率 $=\frac{\mathit{当年专利授权量}-\mathit{上一年专利授权量}}{\mathit{上一年专利授权量}}\times 100\%$，所以只要专利授权量年增长率大于零，当年专利授权量就一定增加． 　 　

③通过统计数据，可以看出长春市区域科技创新力呈上升趋势，为国家科技自立自强贡献吉林力量． 　 　

已知A、B两地之间有一条长440千米的高速公路．甲、乙两车分别从A、B两地同时出发，沿此公路相向而行，甲车先以100千米/时的速度匀速行驶200千米后与乙车相遇，再以另一速度继续匀速行驶4小时到达B地；乙车匀速行驶至A地，两车到达各自的目的地后停止，两车距A地的路程y（千米）与各自的行驶时间x（时）之间的函数关系如图所示．

（1）m＝　 　，n＝　 　；

（2）求两车相遇后，甲车距A地的路程y与x之间的函数关系式；

（3）当乙车到达A地时，求甲车距A地的路程．

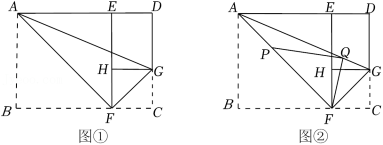
【探索发现】在一次折纸活动中，小亮同学选用了常见的A4纸，如图①，矩形ABCD为它的示意图．他查找了A4纸的相关资料，根据资料显示得出图①中 $AD=\sqrt{2}AB$．他先将A4纸沿过点A的直线折叠，使点B落在AD上，点B的对应点为点E，折痕为AF；再沿过点F的直线折叠，使点C落在EF上，点C的对应点为点H，折痕为FG；然后连结AG，沿AG所在的直线再次折叠，发现点D与点F重合，进而猜想 $△ADG≌△AFG$．

【问题解决】小亮对上面△ADG≌△AFG的猜想进行了证明，下面是部分证明过程：

证明：∵四边形ABCD是矩形，

∴ $\angle BAD＝\angle B＝\angle C＝\angle D＝90°$．

由折叠可知， $\angle BAF=\frac{1}{2}\angle BAD＝45°$， $\angle BFA＝\angle EFA$．

∴ $\angle EFA＝\angle BFA＝45°$．

∴ $AF=\sqrt{2}AB=AD$

请你补全余下的证明过程．

【结论应用】

（1）∠DAG的度数为 　 　度， $\frac{\mathit{FG}}{\mathit{AF}}$的值为 　 　；

（2）在图①的条件下，点P在线段AF上，且AP $=\frac{1}{2}$AB，点Q在线段AG上，连结FQ、PQ，如图②．设 $AB＝a$，则 $FQ+PQ$的最小值为 　 　．（用含a的代数式表示）

如图，在▱ABCD中， $AB＝4$， $AD＝BD=\sqrt{13}$，点M为边AB的中点．动点P从点A出发，沿折线 $AD﹣DB$以每秒 $\sqrt{13}$个单位长度的速度向终点B运动，连结PM．作点A关于直线PM的对称点 $A`$，连结 $A`P$、 $A`M$．设点P的运动时间为t秒，

（1）点D到边AB的距离为 　 　；

（2）用含t的代数式表示线段DP的长；

（3）连结 $A`D$，当线段 $A`D$最短时，求 $△DPA`$的面积；

（4）当 $M$、 $A`$、 $C$三点共线时，直接写出t的值．

在平面直角坐标系中，抛物线 $y＝x^2﹣bx$（b是常数）经过点（2，0）．点A在抛物线上，且点A的横坐标为m（m≠0）．以点A为中心，构造正方形PQMN，PQ＝2|m|，且PQ⊥x轴．

（1）求该抛物线对应的函数表达式；

（2）若点B是抛物线上一点，且在抛物线对称轴左侧．过点B作x轴的平行线交抛物线于另一点C，连结BC．当BC＝4时，求点B的坐标；

（3）若m＞0，当抛物线在正方形内部的点的纵坐标y随x的增大而增大时，或者y随x的增大而减小时，求m的取值范围；

（4）当抛物线与正方形PQMN的边只有2个交点，且交点的纵坐标之差为 $\frac{3}{4}$时，直接写出m的值．