2020年甘肃省兰州市中考数学试卷

$-\frac{1}{2}$的绝对值是（　　）

A． $\frac{1}{2}$B． $-\frac{1}{2}$C．2D．﹣2

如图，该几何体是由5个形状大小相同的正方体组成，它的俯视图是（　　）

A．B．

C．D．

智能手机已遍及生活中的各个角落，移动产业链条正处于由4G到5G的转折阶段．据中国移动2020年3月公布的数据显示，中国移动5G用户数量约 $31720000$户．将 $31720000$用科学记数法表示为（　　）

A． $0.3172\times {10}^8$B． $3.172\times {10}^8$C． $3.172\times {10}^7$D． $3.172\times {10}^9$

如图， $\mathit{AB}\parallel \mathit{CD}$， $\mathit{AE}\parallel \mathit{CF}$， $\angle A＝50°$，则∠C＝（　　）

A． $40°$B． $50°$C． $60°$D． $70°$

化简： $a（a﹣2）+4a＝$（　　）

A． $a^2+2a$B． $a^2+6a$C． $a^2﹣6a$D． $a^2+4a﹣2$

如图，AB是⊙O的直径，若 $\angle \mathit{BAC}＝20°$，则 $\angle \mathit{ADC}＝$（　　）

A． $40°$B． $60°$C． $70°$D． $80°$

一元二次方程 $x（x﹣2\mathit{）＝}x﹣2$的解是（　　）

A． $x_1＝x_2＝0$B． $x_1＝x_2＝1$C． $x_1＝0，x_2＝2$D． $x_1＝1，x_2＝2$

若点 $A\mathit{（﹣}4，m﹣3）$， $B（2n，1）$关于x轴对称，则（　　）

A． $m＝2，n＝0$B． $m＝2，n\mathit{＝﹣}2$C． $m＝4，n＝2$D． $m＝4，n\mathit{＝﹣}2$

中国古代人民在生产生活中发现了许多数学问题，在《孙子算经》中记载了这样一个问题，大意为：有若干人乘车，若每车乘坐3人，则2辆车无人乘坐；若每车乘坐2人，则9人无车可乘，问共有多少辆车，多少人，设共有x辆车，y人，则可列方程组为（　　）

A． $\left\{\begin{array}{c}3(x-2)=y\\ 2x+9=y\end{array}\right.$B． $\left\{\begin{array}{c}3(x+2)=y\\ 2x+9=y\end{array}\right.$

C． $\left\{\begin{array}{c}3x=y\\ 2x+9=y\end{array}\right.$D． $\left\{\begin{array}{c}3(x+2)=y\\ 2x-9=y\end{array}\right.$

如图，在△ABC中， $\mathit{AB}＝\mathit{AC}$，点D在CA的延长线上， $\mathit{DE}\perp \mathit{BC}$于点E， $\angle \mathit{BAC}＝100°$，则 $\angle D＝$（　　）

A． $40°$B． $50°$C． $60°$D． $80°$

已知点 $A（x_1，y_1）$， $B（x_2，y_2）$在反比例函数 $y\mathit{＝﹣}\frac{3}{x}$的图象上，若 $y_1＜y_2＜0$，则下列结论正确的是（　　）

A． $x_1＜x_2＜0$B． $x_2＜x_1＜0$C． $0＜x_1＜x_2$D． $0＜x_2＜x_1$

如图，在 $\mathit{Rt}△\mathit{ABC}$中， $\angle \mathit{BAC}＝90°$，以点A为圆心，以AB长为半径作弧交BC于点D，再分别以点B，D为圆心，以大于 $\frac{1}{2}\mathit{BD}$的长为半径作弧，两弧交于点P，作射线AP交BC于点E，若 $\mathit{AB}＝3$， $\mathit{AC}＝4$，则 $\mathit{CD}＝$（　　）

A． $\frac{12}{5}$B． $\frac{9}{5}$C． $\frac{8}{5}$D． $\frac{7}{5}$

因式分解： $m^3﹣6m^2+9m＝$　　．

点 $A\mathit{（﹣}4，3）$， $B（0，k）$在二次函数 $y\mathit{＝﹣（}x+2{）}^2+h$的图象上，则 $k＝$　　．

如图，四边形ABCD与四边形 $A\text{'}B\text{'}C\text{'}D\text{'}$位似，位似中心为点O， $\mathit{OC}＝6$， $\mathit{CC}\text{'}＝4$， $\mathit{AB}＝3$，则 $A\text{'}B\text{'}＝$　　．

如图，在正方形ABCD中，对角线AC与BD相交于点O， $\mathit{AB}＝2$，点E在AB的延长线上，且 $\mathit{AE}＝\mathit{AC}$， $\mathit{EF}\perp \mathit{AC}$于点F，连接BF并延长交CD于点G，则 $\mathit{DG}＝$　　．

计算： $\sqrt{2}\times \sqrt{6}-{(\sqrt{3}+1)}^2$

解不等式组： $\left\{\begin{array}{c}2(x+1)>3x-1①\\ \frac{2x-1}{2}>\frac{x+1}{3}②\end{array}\right.$

先化简，再求值： $\left(\frac{3a}{a-2}-\frac{a}{a+2}\right)÷\frac{2a}{a^2-4}$，其中 $a\mathit{＝﹣}\frac{1}{2}$．

如图，在 $△\mathit{ABC}$中， $\mathit{AB}＝\mathit{AC}$，点D，E分别是AC和AB的中点．求证： $\mathit{BD}＝\mathit{CE}$．

某学校组织了以“纪念革命先烈，激发爱国热情”为主题的爱国主义教育研学活动，参加活动的学生可从学校提供的四个研学地点中任选一个，地点如下：

A：陇南市宕昌县哈达铺红军长征纪念馆；

B：陇南市两当兵变纪念馆；

C：甘南州迭部县腊子口战役纪念馆；

D：张掖市高台县中国工农红军西路军纪念馆．

小宁和小丽决定通过抽签的方式确定本次研学活动目的地，请你用树状图或列表的方法求出小宁和小丽抽到同一地点的概率．

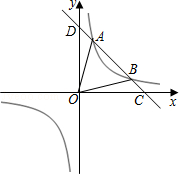
如图，在平面直角坐标系 $\mathit{xOy}$中，一次函数 $y＝\mathit{ax}+b（a\ne 0）$的图象与反比例函数 $y=\frac{k}{x}（k\ne 0，x＞0）$的图象相交于 $A（1，5）$， $B（m，1）$两点，与x轴，y轴分别交于点C，D，连接OA，OB．

（1）求反比例函数 $y=\frac{k}{x}（k\ne 0，x＞0）$和一次函数 $y＝\mathit{ax}+b（a\ne 0）$的表达式；

（2）求 $△\mathit{AOB}$的面积．

如图，在 $\mathit{Rt}△\mathit{AOB}$中， $\angle \mathit{AOB}＝90°$， $\mathit{OA}＝\mathit{OB}$，点C是 $\mathit{AB}$的中点，以OC为半径作 $\odot O$．

（1）求证： $\mathit{AB}$是 $\odot O$的切线；

（2）若 $\mathit{OC}＝2$，求 $\mathit{OA}$的长．

为培养学生正确的劳动价值观和良好劳动品质，加强新时代中学生劳动教育，某校八年级（1）班对本班35名学生进行了劳动能力量化评估和近一周家务劳动总时间调查，并对相关数据进行了收集、整理和分析，研究过程中的部分数据如下：

信息一：劳动能力量化评估的成绩采用十分制，得分均为整数；

信息二：

信息三：

近一周家务劳动时间分布表

信息四：

劳动能力量化成绩与近一周家务劳动总时间统计表

根据以上信息，解决下列问题：

（1）直接从信息二的统计图中“读”出八年级（1）班劳动能力量化成绩的平均分为　　分；

（2）请你判断下列说法合理吗？（请在横线上填写“合理”或“不合理”）

①规定劳动能力量化成绩8分及以上为合格，八年级（1）班超过半数的学生达到了合格要求：　　．

②班主任对近一周家务劳动总时间在4小时以上，且劳动能力量化成绩取得10分的学生进行表彰奖励，恰有3人获奖：　　．

③小颖推断劳动能力量化成绩为8分的同学近一周家务劳动总时间主要分布在 $2＜t\le 3$的时间段：　　．

（3）结合以上信息，你认为普遍情况下参加家务劳动的时间与劳动能力之间具有怎样的关系？

为进一步加强疫情防控工作，避免在测温过程中出现人员聚集现象，某学校决定安装，该设备通过探测人体红外辐射能量对进入测温区域的人员进行快速测温，无需人员停留和接触，安装说明书的部分内容如表．

根据以上内容，解决问题：

学校要求测温区域的宽度AB为4m，请你帮助学校确定该设备的安装高度OC．

（结果精确到0.1m，参考数据： $\mathit{sin}73.14°\approx 0.957，\mathit{cos}73.14°\approx 0.290$，t $\mathit{an}73.14°\approx 3.300$， $\mathit{sin}30.97°\approx 0.515$， $\mathit{cos}30.97°\approx 0.857$， $\text{t}\mathit{an}30.97°\approx 0.600$）

如图1，在 $△\mathit{ABC}$中， $\mathit{AB}＝6\mathit{cm}$， $\mathit{AC}＝5\mathit{cm}$， $\angle \mathit{CAB}＝60°$，点D为AB的中点，线段 $\mathit{AC}$上有一动点E，连接DE，作DA关于直线DE的对称图形，得到 $\mathit{DF}$，过点F作 $\mathit{FG}\perp \mathit{AB}$于点G．设A、E两点间的距离为 $\mathit{xcm}$， $F，G$两点间的距离为 $\mathit{ycm}．$

小军根据学习函数的经验，对因变量y随自变量x的变化而变化的规律进行了探究．

下面是小军的探究过程，请补充完整．

（1）列表：如表的已知数据是根据A，E两点间的距离x进行取点、画图、测量，分别得到了x与y的几组对应值：

请你通过计算补全表格；

（2）描点、连线：在平面直角坐标系 $\mathit{xOy}$中（如图2），描出表中各组数值所对应的点 $（x，y）$，并画出y关于x的图象；

（3）探究性质：随着x值的不断增大，y的值是怎样变化的？　　；

（4）解决问题：当 $\mathit{AE}+\mathit{FG}＝2$时，FG的长度大约是　　cm（保留两位小数）．

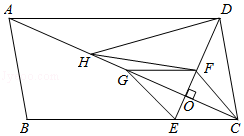
如图，在 $▱\mathit{ABCD}$中， $\mathit{DE}\perp \mathit{AC}$于点O，交BC于点E， $\mathit{EG}＝\mathit{EC}$， $\mathit{GF}\parallel \mathit{AD}$交DE于点F，连接 $\mathit{FC}$，点H为线段 $\mathit{AO}$上一点，连接 $\mathit{HD}，\mathit{HF}$．

（1）判断四边形 $\mathit{GECF}$的形状，并说明理由；

（2）当 $\angle \mathit{DHF}＝\angle \mathit{HAD}$时，求证： $\mathit{AH}•\mathit{CH}＝\mathit{EC}•\mathit{AD}$．

如图，二次函数 $y＝\frac{1}{4}{x}^2+\mathit{bx}+c$的图象过点 $A（4\mathit{，﹣}4）$， $B\mathit{（﹣}2，m）$，交y轴于点 $C（0\mathit{，﹣}4）$．直线BO与抛物线相交于另一点D，连接 $\mathit{AB}，\mathit{AD}$，点E是线段AB上的一动点，过点E作 $\mathit{EF}\parallel \mathit{BD}$交AD于点F．

（1）求二次函数 $y＝\frac{1}{4}{x}^2+\mathit{bx}+c$的表达式；

（2）判断 $△\mathit{AB}D$的形状，并说明理由；

（3）在点E的运动过程中，直线 $\mathit{BD}$上存在一点G，使得四边形AFGE为矩形，请判断此时 $\mathit{AG}与\mathit{BD}$的数量关系，并求出点E的坐标；

（4）点H是抛物线的顶点，在（3）的条件下，点P是平面内使得 $\angle \mathit{EPF}＝90°$的点，在抛物线的对称轴上，是否存在点Q，使得 $△\mathit{HPQ}$是以 $\angle \mathit{PQH}$为直角的等腰直角三角形，若存在，直接写出符合条件的所有点Q的坐标；若不存在，请说明理由．