2020年山东省德州市中考数学试卷
如图1是用5个相同的正方体搭成的立体图形.若由图1变化至图2,则三视图中没有发生变化的是

A.主视图B.主视图和左视图
C.主视图和俯视图D.左视图和俯视图
为提升学生的自理和自立能力,李老师调查了全班学生在一周内的做饭次数情况,调查结果如下表:
一周做饭次数 |
4 |
5 |
6 |
7 |
8 |
人数 |
7 |
6 |
12 |
10 |
5 |
那么一周内该班学生的平均做饭次数为
A.4B.5C.6D.7
如图,小明从 点出发,沿直线前进8米后向左转 ,再沿直线前进8米,又向左转 照这样走下去,他第一次回到出发点 时,共走路程为

A.80米B.96米C.64米D.48米
下列命题:
①一组对边平行,另一组对边相等的四边形是平行四边形;
②对角线互相垂直且平分的四边形是菱形;
③一个角为 且一组邻边相等的四边形是正方形;
④对角线相等的平行四边形是矩形.
其中真命题的个数是
A.1B.2C.3D.4
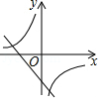
二次函数 的部分图象如图所示,则下列选项错误的是
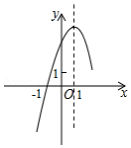
A.若 , 是图象上的两点,则
B.
C.方程 有两个不相等的实数根
D.当 时, 随 的增大而减小
如图是用黑色棋子摆成的美丽图案,按照这样的规律摆下去,第10个这样的图案需要黑色棋子的个数为

A.148B.152C.174D.202
在平面直角坐标系中,点 的坐标是 ,以原点 为位似中心,把线段 放大为原来的2倍,点 的对应点为 .若点 恰在某一反比例函数图象上,则该反比例函数解析式为 .
如图,在 的正方形网格中,有4个小正方形已经涂黑,若再涂黑任意1个白色的小正方形(每个白色小正方形被涂黑的可能性相同),使新构成的黑色部分图形是轴对称图形的概率是 .

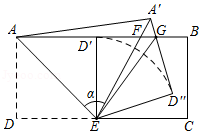
如图,在矩形 中, , .把 沿 折叠,使点 恰好落在 边上的 处,再将 绕点 顺时针旋转 ,得到△ ,使得 恰好经过 的中点 . 交 于点 ,连接 .有如下结论:① 的长度是 ;②弧 的长度是 ;③△ △ ;④△ .上述结论中,所有正确的序号是 .
某校"校园主持人大赛"结束后,将所有参赛选手的比赛成绩(得分均为整数)进行整理,并分别绘制成扇形统计图和频数直方图.部分信息如下:

(1)本次比赛参赛选手共有 人,扇形统计图中" "这一范围的人数占总参赛人数的百分比为 ;
(2)补全图2频数直方图;
(3)赛前规定,成绩由高到低前 的参赛选手获奖.某参赛选手的比赛成绩为88分,试判断他能否获奖,并说明理由;
(4)成绩前四名是2名男生和2名女生,若从他们中任选2人作为该校文艺晚会的主持人,试求恰好选中1男1女为主持人的概率.
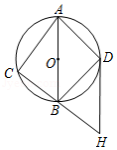
如图,点 在以 为直径的 上,点 是半圆 的中点,连接 , , , .过点 作 交 的延长线于点 .
(1)求证:直线 是 的切线;
(2)若 , ,求 , 的长.
小刚去超市购买画笔,第一次花60元买了若干支 型画笔,第二次超市推荐了 型画笔,但 型画笔比 型画笔的单价贵2元,他又花100元买了相同支数的 型画笔.
(1)超市 型画笔单价多少元?
(2)小刚使用两种画笔后,决定以后使用 型画笔,但感觉其价格稍贵,和超市沟通后,超市给出以下优惠方案:一次购买不超过20支,则每支 型画笔打九折;若一次购买超过20支,则前20支打九折,超过的部分打八折.设小刚购买的 型画笔 支,购买费用为 元,请写出 关于 的函数关系式.
(3)在(2)的优惠方案下,若小刚计划用270元购买 型画笔,则能购买多少支 型画笔?
问题探究:
小红遇到这样一个问题:如图1, 中, , , 是中线,求 的取值范围.她的做法是:延长 到 ,使 ,连接 ,证明 ,经过推理和计算使问题得到解决.
请回答:(1)小红证明 的判定定理是: ;
(2) 的取值范围是 ;
方法运用:
(3)如图2, 是 的中线,在 上取一点 ,连结 并延长交 于点 ,使 ,求证: .
(4)如图3,在矩形 中, ,在 上取一点 ,以 为斜边作 ,且 ,点 是 的中点,连接 , ,求证: .

如图1,在平面直角坐标系中,点 的坐标是 ,在 轴上任取一点 ,连接 ,分别以点 和点 为圆心,大于 的长为半径作弧,两弧相交于 , 两点,作直线 ,过点 作 轴的垂线 交直线 于点 .根据以上操作,完成下列问题.
探究:
(1)线段 与 的数量关系为 ,其理由为: .
(2)在 轴上多次改变点 的位置,按上述作图方法得到相应点 的坐标,并完成下列表格:
的坐标 |
|
|
|
|
|
|
的坐标 |
|
|
|
|
|
|
猜想:
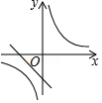
(3)请根据上述表格中 点的坐标,把这些点用平滑的曲线在图2中连接起来;观察画出的曲线 ,猜想曲线 的形状是 .
验证:
(4)设点 的坐标是 ,根据图1中线段 与 的关系,求出 关于 的函数解析式.
应用:
(5)如图3,点 , ,点 为曲线 上任意一点,且 ,求点 的纵坐标 的取值范围.

 B.
B. C.
C. D.
D.
 B.
B.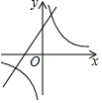
 D.
D.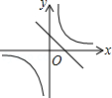


 粤公网安备 44130202000953号
粤公网安备 44130202000953号