2018年浙江省金华市(丽水市)中考数学试卷
如图,一个游戏转盘中,红、黄、蓝三个扇形的圆心角度数分别为 , , .让转盘自由转动,指针停止后落在黄色区域的概率是
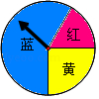
A. B. C. D.
小明为画一个零件的轴截面,以该轴截面底边所在的直线为 轴,对称轴为 轴,建立如图所示的平面直角坐标系.若坐标轴的单位长度取 ,则图中转折点 的坐标表示正确的是

A. B. C. D.
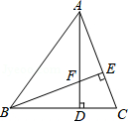
如图,将 绕点 顺时针旋转 得到 .若点 , , 在同一条直线上, ,则 的度数是

A. B. C. D.
某通讯公司就上宽带网推出 , , 三种月收费方式.这三种收费方式每月所需的费用 (元 与上网时间 的函数关系如图所示,则下列判断错误的是

A.每月上网时间不足 时,选择 方式最省钱
B.每月上网费用为60元时, 方式可上网的时间比 方式多
C.每月上网时间为 时,选择 方式最省钱
D.每月上网时间超过 时,选择 方式最省钱
如图2,小靓用七巧板拼成一幅装饰图,放入长方形 内,装饰图中的三角形顶点 , 分别在边 , 上,三角形①的边 在边 上,则 的值是 .
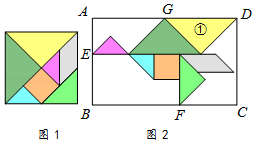
如图1是小明制作的一副弓箭,点 , 分别是弓臂 与弓弦 的中点,弓弦 .沿 方向拉动弓弦的过程中,假设弓臂 始终保持圆弧形,弓弦不伸长.如图2,当弓箭从自然状态的点 拉到点 时,有 , .
(1)图2中,弓臂两端 , 的距离为 .
(2)如图3,将弓箭继续拉到点 ,使弓臂 为半圆,则 的长为 .

为了解朝阳社区 岁居民最喜欢的支付方式,某兴趣小组对社区内该年龄段的部分居民展开了随机问卷调查(每人只能选择其中一项),并将调查数据整理后绘成如下两幅不完整的统计图.请根据图中信息解答下列问题:
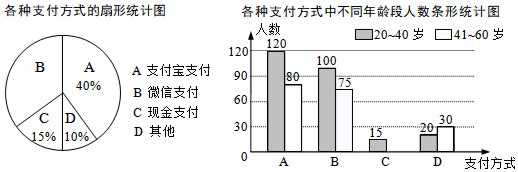
(1)求参与问卷调查的总人数.
(2)补全条形统计图.
(3)该社区中 岁的居民约8000人,估算这些人中最喜欢微信支付方式的人数.
如图,在 的网格中,每个小正方形的边长为1,点 在格点(小正方形的顶点)上.试在各网格中画出顶点在格点上,面积为6,且符合相应条件的图形.
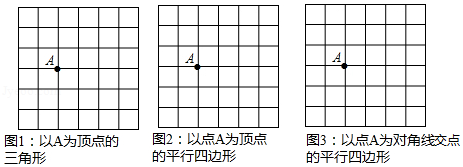
如图,在 中,点 在斜边 上,以 为圆心, 为半径作圆,分别与 , 相交于点 , ,连接 .已知 .
(1)求证: 是 的切线.
(2)若 , ,求 的半径.

如图,抛物线 过点 ,矩形 的边 在线段 上(点 在点 的左边),点 , 在抛物线上.设 ,当 时, .
(1)求抛物线的函数表达式.
(2)当 为何值时,矩形 的周长有最大值?最大值是多少?
(3)保持 时的矩形 不动,向右平移抛物线.当平移后的抛物线与矩形的边有两个交点 , ,且直线 平分矩形的面积时,求抛物线平移的距离.

如图,四边形 的四个顶点分别在反比例函数 与 的图象上,对角线 轴,且 于点 .已知点 的横坐标为4.
(1)当 , 时.
①若点 的纵坐标为2,求直线 的函数表达式.
②若点 是 的中点,试判断四边形 的形状,并说明理由.
(2)四边形 能否成为正方形?若能,求此时 , 之间的数量关系;若不能,试说明理由.






 粤公网安备 44130202000953号
粤公网安备 44130202000953号