2018年四川省自贡市中考数学试卷
2017年我市用于资助贫困学生的助学金总额是445800000元,将445800000用科学记数法表示为
A. B. C. D.
在一次数学测试后,随机抽取九年级(3)班5名学生的成绩(单位:分)如下:80、98、98、83、91,关于这组数据的说法错误的是
A.众数是98B.平均数是90C.中位数是91D.方差是56
回顾初中阶段函数的学习过程,从函数解析式到函数图象,再利用函数图象研究函数的性质,这种研究方法主要体现的数学思想是
A.数形结合B.类比C.演绎D.公理化
如图,在边长为 正方形 中,把边 绕点 逆时针旋转 ,得到线段 ,连接 并延长交 于 ,连接 ,则 的面积为

A. B. C. D.
六一儿童节,某幼儿园用100元钱给小朋友买了甲、乙两种不同的玩具共30个,单价分别为2元和4元,则该幼儿园购买了甲、乙两种玩具分别为 、 个.
如图,在 中, , ,将它沿 翻折得到 ,则四边形 的形状是 形,点 、 、 分别为线段 、 、 的任意点,则 的最小值是 .

某校研究学生的课余爱好情况,采取抽样调查的方法,从阅读、运动、娱乐、上网等四个方面调查了若干名学生的兴趣爱好,并将调查结果绘制成下面两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
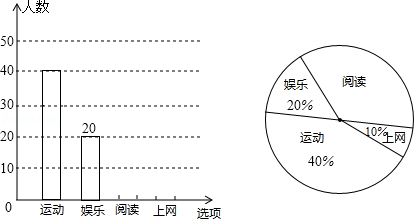
(1)在这次调查中,一共调查了 名学生;
(2)补全条形统计图;
(3)若该校共有1500名学生,估计爱好运动的学生有 人;
(4)在全校同学中随机选取一名学生参加演讲比赛,用频率估计概率,则选出的恰好是爱好阅读的学生的概率是 .
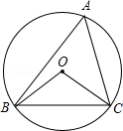
如图,在 中, .
(1)作出经过点 ,圆心 在斜边 上且与边 相切于点 的 (要求:用尺规作图,保留作图痕迹,不写作法和证明)
(2)设(1)中所作的 与边 交于异于点 的另外一点 ,若 的直径为5, ;求 的长.(如果用尺规作图画不出图形,可画出草图完成(2)问)

阅读以下材料:
对数的创始人是苏格兰数学家纳皮尔 . , 年),纳皮尔发明对数是在指数书写方式之前,直到18世纪瑞士数学家欧拉 , 年)才发现指数与对数之间的联系.
对数的定义:一般地,若 ,那么 叫做以 为底 的对数,记作: .比如指数式 可以转化为 ,对数式 可以转化为 .
我们根据对数的定义可得到对数的一个性质: , , , ;理由如下:
设 , ,则 ,
,由对数的定义得
又
解决以下问题:
(1)将指数 转化为对数式 ;
(2)证明 , , ,
(3)拓展运用:计算 .
如图,已知 ,在 的平分线 上有一点 ,将一个 角的顶点与点 重合,它的两条边分别与直线 、 相交于点 、 .
(1)当 绕点 旋转到 与 垂直时(如图 ,请猜想 与 的数量关系,并说明理由;
(2)当 绕点 旋转到 与 不垂直时,到达图2的位置,(1)中的结论是否成立?并说明理由;
(3)当 绕点 旋转到 与 的反向延长线相交时,上述结论是否成立?请在图3中画出图形,若成立,请给于证明;若不成立,线段 、 与 之间又有怎样的数量关系?请写出你的猜想,不需证明.



 B.
B. C.
C. D.
D.

 B.
B.
 D.
D.


 粤公网安备 44130202000953号
粤公网安备 44130202000953号