2018年四川省乐山市中考数学试卷
下列调查中,适宜采用普查方式的是
A.调查全国中学生心理健康现状
B.调查一片试验田里某种大麦的穗长情况
C.调查冷饮市场上冰淇淋的质量情况
D.调查你所在班级的每一个同学所穿鞋子的尺码情况
《九章算术》是我国古代第一部自成体系的数学专著,代表了东方数学的最高成就.它的算法体系至今仍在推动着计算机的发展和应用.书中记载:“今有圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”译为:“今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯这木材,锯口深1寸 寸),锯道长1尺 尺 寸)”,问这块圆柱形木材的直径是多少?”
如图所示,请根据所学知识计算:圆柱形木材的直径 是

A.13寸B.20寸C.26寸D.28寸
如图,曲线 是双曲线 绕原点 逆时针旋转 得到的图形, 是曲线 上任意一点,点 在直线 上,且 ,则 的面积等于

A. B.6C.3D.12
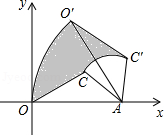
如图, 的顶点 在坐标原点, 边在 轴上, , ,把 绕点 按顺时针方向旋转到△ ,使得点 的坐标是 ,则在旋转过程中线段 扫过部分(阴影部分)的面积为 .
已知直线 和直线 ,其中 为不小于2的自然数.
(1)当 时,直线 、 与 轴围成的三角形的面积 ;
(2)当 、3、4, ,2018时,设直线 、 与 轴围成的三角形的面积分别为 , , , , ,则 .
某校八年级甲、乙两班各有学生50人,为了了解这两个班学生身体素质情况,进行了抽样调查,过程如下,请补充完整.
(1)收集数据
从甲、乙两个班各随机抽取10名学生进行身体素质测试,测试成绩(百分制)如下:
甲班65 75 75 80 60 50 75 90 85 65
乙班90 55 80 70 55 70 95 80 65 70
(2)整理描述数据
按如下分数段整理、描述这两组样本数据:
成绩 人数 班级 |
|
|
|
|
|
甲班 |
1 |
3 |
3 |
2 |
1 |
乙班 |
2 |
1 |
|
2 |
|
在表中: , .
(3)分析数据
①两组样本数据的平均数、中位数、众数如表所示:
班级 |
平均数 |
中位数 |
众数 |
甲班 |
72 |
|
75 |
乙班 |
73 |
70 |
|
在表中: , .
②若规定测试成绩在80分(含80分)以上的学生身体素质为优秀,请估计乙班50名学生中身体素质为优秀的学生有 人.
③现从甲班指定的2名学生 男1女),乙班指定的3名学生 男1女)中分别抽取1名学生去参加上级部门组织的身体素质测试,用树状图和列表法求抽到的2名同学是1男1女的概率.
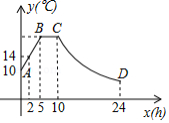
某蔬菜生产基地的气温较低时,用装有恒温系统的大棚栽培一种新品种蔬菜.如图是试验阶段的某天恒温系统从开启到关闭后,大棚内的温度 与时间 之间的函数关系,其中线段 、 表示恒温系统开启阶段,双曲线的一部分 表示恒温系统关闭阶段.
请根据图中信息解答下列问题:
(1)求这天的温度 与时间 的函数关系式;
(2)求恒温系统设定的恒定温度;
(3)若大棚内的温度低于 时,蔬菜会受到伤害.问这天内,恒温系统最多可以关闭多少小时,才能使蔬菜避免受到伤害?
已知关于 的一元二次方程 .
(1)求证:无论 为任何非零实数,此方程总有两个实数根;
(2)若抛物线 与 轴交于 , 、 , 两点,且 ,求 的值;
(3)若 ,点 与 在(2)中的抛物线上(点 、 不重合),求代数式 的值.
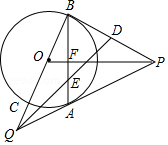
如图, 是 外的一点, 、 是 的两条切线, 、 是切点, 交 于点 ,延长 交 于点 ,交 的延长交于点 ,连接 .
(1)求证: ;
(2)设 为 的中点, 交 于点 ,若 的半径为3, ,求 的值.
已知 中, ,点 、 分别在 、 边上,连接 、 交于点 ,设 , , 为常数,试探究 的度数:
(1)如图1,若 ,则 的度数为 ;
(2)如图2,若 ,试问(1)中的结论是否成立?若成立,请说明理由;若不成立,求出 的度数.
(3)如图3,若 ,且 、 分别在 、 的延长线上,(2)中的结论是否成立,请说明理由.

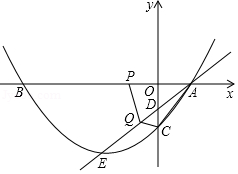
如图,在平面直角坐标系中,抛物线 交 轴于 、 两点,交 轴于点 , , ,直线 过点 ,交 轴于点 ,交抛物线于点 ,且满足 .
(1)求抛物线的解析式;
(2)动点 从点 出发,沿 轴正方向以每秒2个单位长度的速度向点 运动,动点 从点 出发,沿射线 以每秒1个单位长度的速度向点 运动,当点 运动到点 时,点 也停止运动,设运动时间为 秒.
①在 、 的运动过程中,是否存在某一时刻 ,使得 与 相似,若存在,求出 的值;若不存在,请说明理由.
②在 、 的运动过程中,是否存在某一时刻 ,使得 与 的面积之和最大?若存在,求出 的值;若不存在,请说明理由.

 B.
B.
 D.
D.



 粤公网安备 44130202000953号
粤公网安备 44130202000953号