2018年山东省济南市中考数学试卷

数4的算术平方根是 $($　　 $)$

A．2B． $-2$C． $\pm 2$D． $\sqrt{2}$

如图所示的几何体，它的俯视图是 $($　　 $)$

A．B．

C．D．

2018年1月，“墨子号”量子卫星实现了距离达7600千米的洲际量子密钥分发，这标志着“墨子号”具备了洲际量子保密通信的能力．数字7600用科学记数法表示为 $($　　 $)$

A． $0.76\times {10}^4$B． $7.6\times {10}^3$C． $7.6\times {10}^4$D． $76\times {10}^2$

“瓦当”是中国古建筑装饰檐头的附件，是中国特有的文化艺术遗产，下面“瓦当”图案中既是轴对称图形又是中心对称图形的是 $($　　 $)$

A．B．

C．D．

如图， $\mathit{AF}$是 $\angle \mathit{BAC}$的平分线， $\mathit{DF}//\mathit{AC}$，若 $\angle 1=35°$，则 $\angle \mathit{BAF}$的度数为 $($　　 $)$

A． $17.5°$B． $35°$C． $55°$D． $70°$

下列运算正确的是 $($　　 $)$

A． $a^2+2a=3a^3$B． ${(-2a^3)}^2=4a^5$

C． $(a+2)(a-1)=a^2+a-2$D． ${(a+b)}^2=a^2+b^2$

关于 $x$的方程 $3x-2m=1$的解为正数，则 $m$的取值范围是 $($　　 $)$

A． $m<-\frac{1}{2}$B． $m>-\frac{1}{2}$C． $m>\frac{1}{2}$D． $m<\frac{1}{2}$

在反比例函数 $y=-\frac{2}{x}$图象上有三个点 $A(x_1$， $y_1)$、 $B(x_2$， $y_2)$、 $C(x_3$， $y_3)$，若 $x_1<0<x_2<x_3$，则下列结论正确的是 $($　　 $)$

A． $y_3<y_2<y_1$B． $y_1<y_3<y_2$C． $y_2<y_3<y_1$D． $y_3<y_1<y_2$

如图，在平面直角坐标系中， $\mathit{\Delta ABC}$的顶点都在方格线的格点上，将 $\mathit{\Delta ABC}$绕点 $P$顺时针方向旋转 $90°$，得到△ $A\text{'}B\text{'}C\text{'}$，则点 $P$的坐标为 $($　　 $)$

A． $(0,4)$B． $(1,1)$C． $(1,2)$D． $(2,1)$

下面的统计图大致反应了我国2012年至2017年人均阅读量的情况．根据统计图提供的信息，下列推断不合理的是 $($　　 $)$

A．与2016年相比，2017年我国电子书人均阅读量有所降低

B．2012年至2017年，我国纸质书的人均阅读量的中位数是4.57

C．从2014年到2017年，我国纸质书的人均阅读量逐年增长

D．2013年我国纸质书的人均阅读量比电子书的人均阅读量的1.8倍还多

如图1，一个扇形纸片的圆心角为 $90°$，半径为6．如图2，将这张扇形纸片折叠，使点 $A$与点 $O$恰好重合，折痕为 $\mathit{CD}$，图中阴影为重合部分，则阴影部分的面积为 $($　　 $)$

A． $6\pi -\frac{9}{2}\sqrt{3}$B． $6\pi -9\sqrt{3}$C． $12\pi -\frac{9}{2}\sqrt{3}$D． $\frac{9\pi }{4}$

若平面直角坐标系内的点 $M$满足横、纵坐标都为整数，则把点 $M$叫做“整点”．例如： $P(1,0)$、 $Q(2,-2)$都是“整点”．抛物线 $y=m{x}^2-4\mathit{mx}+4m-2(m>0)$与 $x$轴交于点 $A$、 $B$两点，若该抛物线在 $A$、 $B$之间的部分与线段 $\mathit{AB}$所围成的区域（包括边界）恰有七个整点，则 $m$的取值范围是 $($　　 $)$

A． $\frac{1}{2}⩽m<1$B． $\frac{1}{2}<m⩽1$C． $1<m⩽2$D． $1<m<2$

分解因式： $m^2-4=$　　．

在不透明的盒子中装有5个黑色棋子和若干个白色棋子，每个棋子除颜色外都相同，任意摸出一个棋子，摸到黑色棋子的概率是 $\frac{1}{4}$，则白色棋子的个数是　　．

一个正多边形的每个内角等于 $108°$，则它的边数是　　．

若代数式 $\frac{x-2}{x-4}$的值是2，则 $x=$　　．

$A$、 $B$两地相距 $20\mathit{km}$，甲乙两人沿同一条路线从 $A$地到 $B$地．甲先出发，匀速行驶，甲出发1小时后乙再出发，乙以 $2\mathit{km}/h$的速度匀速行驶1小时后提高速度并继续匀速行驶，结果比甲提前到达．甲、乙两人离开 $A$地的距离 $y\left(\mathit{km}\right)$与时间 $t\left(h\right)$的关系如图所示，则甲出发　　小时后和乙相遇．

如图，矩形 $\mathit{EFGH}$的四个顶点分别在矩形 $\mathit{ABCD}$的各条边上， $\mathit{AB}=\mathit{EF}$， $\mathit{FG}=2$， $\mathit{GC}=3$．有以下四个结论：① $\angle \mathit{BGF}=\angle \mathit{CHG}$；② $\mathit{\Delta BFG}\cong \mathit{\Delta DHE}$；③ $\tan \angle \mathit{BFG}=\frac{1}{2}$；④矩形 $\mathit{EFGH}$的面积是 $4\sqrt{3}$．其中一定成立的是　　．（把所有正确结论的序号填在横线上）

计算： $2^{-1}+|-5|-\sin 30°+{(\pi -1)}^0$．

解不等式组： $\left\{\begin{array}{c}3x+1<2x+3①\\ 2x>\frac{3x-1}{2}②\end{array}\right.$

如图，在 $▱\mathit{ABCD}$中，连接 $\mathit{BD}$， $E$是 $\mathit{DA}$延长线上的点， $F$是 $\mathit{BC}$延长线上的点，且 $\mathit{AE}=\mathit{CF}$，连接 $\mathit{EF}$交 $\mathit{BD}$于点 $O$．求证： $\mathit{OB}=\mathit{OD}$．

本学期学校开展以“感受中华传统美德”为主题的研学活动，组织150名学生参观历史博物馆和民俗展览馆，每一名学生只能参加其中一项活动，共支付票款2000元，票价信息如下：

（1）请问参观历史博物馆和民俗展览馆的人数各是多少人？

（2）若学生都去参观历史博物馆，则能节省票款多少元？

如图 $\mathit{AB}$是 $\odot O$的直径， $\mathit{PA}$与 $\odot O$相切于点 $A$， $\mathit{BP}$与 $\odot O$相交于点 $D$， $C$为 $\odot O$上的一点，分别连接 $\mathit{CB}$、 $\mathit{CD}$， $\angle \mathit{BCD}=60°$．

（1）求 $\angle \mathit{ABD}$的度数；

（2）若 $\mathit{AB}=6$，求 $\mathit{PD}$的长度．

某校开设了“ $3D$”打印、数学史、诗歌欣赏、陶艺制作四门校本课程，为了解学生对这四门校本课程的喜爱情况，对学生进行了随机问卷调查（问卷调查表如图所示），将调查结果整理后绘制例图1、图2两幅均不完整的统计图表．

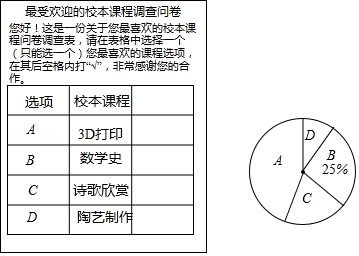
请您根据图表中提供的信息回答下列问题：

（1）统计表中的 $a=$　   ， $b=$　　；

（2）“ $D$”对应扇形的圆心角为　　度；

（3）根据调查结果，请您估计该校2000名学生中最喜欢“数学史”校本课程的人数；

（4）小明和小亮参加校本课程学习，若每人从“ $A$”、“ $B$”、“ $C$”三门校本课程中随机选取一门，请用画树状图或列表格的方法，求两人恰好选中同一门校本课程的概率．

如图，直线 $y=\mathit{ax}+2$与 $x$轴交于点 $A(1,0)$，与 $y$轴交于点 $B(0,b)$．将线段 $\mathit{AB}$先向右平移1个单位长度、再向上平移 $t(t>0)$个单位长度，得到对应线段 $\mathit{CD}$，反比例函数 $y=\frac{k}{x}(x>0)$的图象恰好经过 $C$、 $D$两点，连接 $\mathit{AC}$、 $\mathit{BD}$．

（1）求 $a$和 $b$的值；

（2）求反比例函数的表达式及四边形 $\mathit{ABDC}$的面积；

（3）点 $N$在 $x$轴正半轴上，点 $M$是反比例函数 $y=\frac{k}{x}(x>0)$的图象上的一个点，若 $\mathit{\Delta CMN}$是以 $\mathit{CM}$为直角边的等腰直角三角形时，求所有满足条件的点 $M$的坐标．

在 $\mathit{\Delta ABC}$中， $\mathit{AB}=\mathit{AC}$， $\angle \mathit{BAC}=120°$，以 $\mathit{CA}$为边在 $\angle \mathit{ACB}$的另一侧作 $\angle \mathit{ACM}=\angle \mathit{ACB}$，点 $D$为射线 $\mathit{BC}$上任意一点，在射线 $\mathit{CM}$上截取 $\mathit{CE}=\mathit{BD}$，连接 $\mathit{AD}$、 $\mathit{DE}$、 $\mathit{AE}$．

（1）如图1，当点 $D$落在线段 $\mathit{BC}$的延长线上时，直接写出 $\angle \mathit{ADE}$的度数；

（2）如图2，当点 $D$落在线段 $\mathit{BC}$（不含边界）上时， $\mathit{AC}$与 $\mathit{DE}$交于点 $F$，请问（1）中的结论是否仍成立？如果成立，请给出证明；如果不成立，请说明理由；

（3）在（2）的条件下，若 $\mathit{AB}=6$，求 $\mathit{CF}$的最大值．

如图1，抛物线 $y=a{x}^2+\mathit{bx}+4$过 $A(2,0)$、 $B(4,0)$两点，交 $y$轴于点 $C$，过点 $C$作 $x$轴的平行线与抛物线上的另一个交点为 $D$，连接 $\mathit{AC}$、 $\mathit{BC}$．点 $P$是该抛物线上一动点，设点 $P$的横坐标为 $m(m>4)$．

（1）求该抛物线的表达式和 $\angle \mathit{ACB}$的正切值；

（2）如图2，若 $\angle \mathit{ACP}=45°$，求 $m$的值；

（3）如图3，过点 $A$、 $P$的直线与 $y$轴于点 $N$，过点 $P$作 $\mathit{PM}\perp \mathit{CD}$，垂足为 $M$，直线 $\mathit{MN}$与 $x$轴交于点 $Q$，试判断四边形 $\mathit{ADMQ}$的形状，并说明理由．