2018年山东省德州市中考数学试卷
一年之中地球与太阳之间的距离随时间而变化,1个天文单位是地球与太阳之间的平均距离,即1.496亿 ,用科学记数法表示1.496亿是
A. B.
C. D.
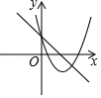
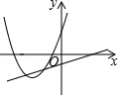
给出下列函数:① ;② ;③ ;④ ,上述函数中符合条件“当 时,函数值 随自变量 增大而增大“的是
A.①③B.③④C.②④D.②③
我国南宋数学家杨辉所著的《详解九章算术》一书中,用如图的三角形解释二项式 的展开式的各项系数,此三角形称为“杨辉三角”

根据”杨辉三角”请计算 的展开式中从左起第四项的系数为
A.84B.56C.35D.28
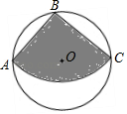
如图,等边三角形 的边长为4,点 是 的中心, ,绕点 旋转 ,分别交线段 、 于 、 两点,连接 ,给出下列四个结论:① ;② ;③四边形 的面积始终等于 ;④ 周长的最小值为6.上述结论中正确的个数是

A.1B.2C.3D.4
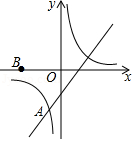
如图,反比例函数 与一次函数 在第三象限交于点 ,点 的坐标为 ,点 是 轴左侧的一点,若以 , , , 为顶点的四边形为平行四边形,则点 的坐标为 .
某学校为了解全校学生对电视节目的喜爱情况(新闻,体育,动画,娱乐,戏曲),从全校学生中随机抽取部分学生进行问卷调查,并把调查结果绘制成两幅不完整的统计图.

请根据以上信息,解答下列问题:
(1)这次被调查的学生共有多少人?
(2)请将条形统计图补充完整;
(3)若该校约有1500名学生,估计全校学生中喜欢娱乐节目的有多少人?
(4)该校广播站需要广播员,现决定从喜欢新闻节目的甲、乙、丙、丁四名同学中选取2名,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答).
如图,两座建筑物的水平距离 为 ,从 点测得 点的仰角 为 ,从 点测得 点的俯角 为 ,求两座建筑物的高度(参考数据: , , , , , .

如图, 是 的直径, 直线 与 相切于点 ,且与 的延长线交于点 ,点 是 的中点 .
(1) 求证: ;
(2) 若 , 的半径为 3 ,一只蚂蚁从点 出发, 沿着 爬回至点 ,求蚂蚁爬过的路程 , , 结果保留一位小数) .

为积极响应新旧动能转换,提高公司经济效益,某科技公司近期研发出一种新型高科技设备,每台设备成本价为30万元,经过市场调研发现,每台售价为40万元时,年销售量为600台;每台售价为45万元时,年销售量为550台.假定该设备的年销售量 (单位:台)和销售单价 (单位:万元)成一次函数关系.
(1)求年销售量 与销售单价 的函数关系式;
(2)根据相关规定,此设备的销售单价不得高于70万元,如果该公司想获得10000万元的年利润,则该设备的销售单价应是多少万元?
再读教材:
宽与长的比是 (约为 的矩形叫做黄金矩形,黄金矩形给我们以协调、匀称的美感,世界各国许多著名的建筑,为取得最佳的视觉效果,都采用了黄金矩形的设计,下面,我们用宽为2的矩形纸片折叠黄金矩形.(提示:
第一步,在矩形纸片一端,利用图①的方法折出一个正方形,然后把纸片展平.
第二步,如图②,把这个正方形折成两个相等的矩形,再把纸片展平.

第三步,折出内侧矩形的对角线 ,并把 折到图③中所示的 处.
第四步,展平纸片,按照所得的点 折出 ,使 ,则图④中就会出现黄金矩形.

问题解决:
(1)图③中 (保留根号);
(2)如图③,判断四边形 的形状,并说明理由;
(3)请写出图④中所有的黄金矩形,并选择其中一个说明理由.
实际操作
(4)结合图④,请在矩形 中添加一条线段,设计一个新的黄金矩形,用字母表示出来,并写出它的长和宽.
 B.
B. C.
C. D.
D.

 B.
B.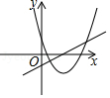
 D.
D.



 粤公网安备 44130202000953号
粤公网安备 44130202000953号