2017年辽宁省抚顺市中考数学试卷
目前,中国网民已经达到731 000 000人,将数据731 000 000用科学记数法表示为
A. B. C. D.
我校四名跳远运动员之前的10次跳远测试中成绩的平均数相同,方差 如表所示,如果要选出一名跳远成绩最稳定的选手参加抚顺市运动会,应选择的选手是
选手 |
甲 |
乙 |
丙 |
丁 |
|
0.5 |
0.5 |
0.6 |
0.4 |
A.甲B.乙C.丙D.丁
为了践行“绿色生活”的理念,甲、乙两人每天骑自行车出行,甲匀速骑行30公里的时间与乙匀速骑行25公里的时间相同,已知甲每小时比乙多骑行2公里,设甲每小时骑行 公里,根据题意列出的方程正确的是
A. B. C. D.
下列事件中是必然事件的是
A.任意画一个正五边形,它是中心对称图形
B.实数 使式子 有意义,则实数
C. , 均为实数,若 , ,则
D.5个数据分别是:6,6,3,2,1,则这组数据的中位数是3
如图,菱形 的边长为2, ,一个以点 为顶点的 角绕点 旋转,这个角的两边分别与线段 的延长线及 的延长线交于点 、 ,设 , ,则能大致反映 与 的函数关系的图象是
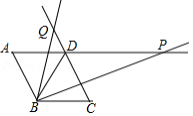
A.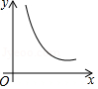 B.
B.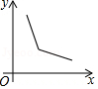
C.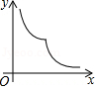 D.
D.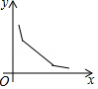
一个不透明的袋中装有除颜色外均相同的9个红球,3个白球,若干个绿球,每次摇匀后随机摸出一个球,记下颜色后再放回袋中,经过大量重复实验后,发现摸到绿球的频率稳定在0.2,则袋中约有绿球 个.
如图,某城市的电视塔 坐落在湖边,数学老师带领学生隔湖测量电视塔 的高度,在点 处测得塔尖点 的仰角 为 ,沿射线 方向前进200米到达湖边点 处,测得塔尖点 在湖中的倒影 的俯角 为 ,则电视塔 的高度为 米(结果保留根号).

如图,等边△ 的周长为1,作 于 ,在 的延长线上取点 ,使 ,连接 ,以 为边作等边△ ;作 于 ,在 的延长线上取点 ,使 ,连接 ,以 为边作等边△ ; 且点 , , , 都在直线 同侧,如此下去,则△ ,△ ,△ , ,△ 的周长和为 . ,且 为整数)

学校想知道九年级学生对我国倡导的“一带一路”的了解程度,随机抽取部分九年级学生进行问卷调查,问卷设有4个选项(每位被调查的学生必选且只选一项) .非常了解. .了解. .知道一点. .完全不知道.将调查的结果绘制如下两幅不完整的统计图,请根据两幅统计图中的信息,解答下列问题:
(1)求本次共调查了多少学生?
(2)补全条形统计图;
(3)该校九年级共有600名学生,请你估计“了解”的学生约有多少名?
(4)在“非常了解”的3人中,有2名女生,1名男生,老师想从这3人中任选两人做宣传员,请用列表或画树状图法求出被选中的两人恰好是一男生一女生的概率.

在平面直角坐标系中, , , 三点坐标分别为 , , .
(1)如图1,顺次连接 , , ,得 .
①点 关于 轴的对称点 的坐标是 ,点 关于 轴的对称点 的坐标是 ;
②画出 关于原点对称的△ ;
③ ;
(2)利用四边形的不稳定性,将第二象限部分由小正方形组成的网格,变化为如图2所示的由小菱形组成的网格,每个小菱形的边长仍为1个单位长度,且较小内角为 ,原来的格点 , , 分别对应新网格中的格点 , , ,顺次连接 , , ,得△ ,则 .

学校准备购进一批篮球和足球,买1个篮球和2个足球共需170元,买2个篮球和1个足球共需190元.
(1)求一个篮球和一个足球的售价各是多少元?
(2)学校欲购进篮球和足球共100个,且足球数量不多于篮球数量的2倍,求出最多购买足球多少个?
如图, 为 直径, 为 的弦,过 外的点 作 于点 ,交 于点 ,连接 并延长交 的延长线于点 ,且 ,作 于点 .
(1)判断直线 与 的位置关系,并说明理由;
(2)若 , ,请求出 的长.

某商场对某种商品进行销售,第 天的销售单价为 元 件,日销售量为 件,其中 , 分别是 ,且 为整数)的一次函数,销售情况如表:
销售第 天 |
第1天 |
第2天 |
第3天 |
第4天 |
|
第30天 |
销售单价 (元 件) |
49 |
48 |
47 |
46 |
|
20 |
日销售量 (件 |
45 |
50 |
55 |
60 |
|
190 |
(1)观察表中数据,分别直接写出 与 , 与 的函数关系式: , ;
(2)求商场销售该商品第几天时该商品的日销售额恰好为3600元?
(3)销售商品的第15天为儿童节,请问:在儿童节前(不包括儿童节当天)销售该商品第几天时该商品的日销售额最多?商场决定将这天该商品的日销售额捐献给儿童福利院,试求出商场可捐款多少元?
如图, 是 的平分线,点 在射线 上, , 是直线 上的两动点,点 在点 的右侧,且 ,作线段 的垂直平分线,分别交直线 、 于点 、点 ,连接 、 .
(1)如图1,当 、 两点都在射线 上时,请直接写出线段 与 的数量关系;
(2)如图2,当 、 两点都在射线 的反向延长线上时,线段 , 是否还存在(1)中的数量关系?若存在,请写出证明过程;若不存在,请说明理由;
(3)如图3, ,连接 ,设 ,当 和 两点都在射线 上移动时, 是否存在最小值?若存在,请直接写出 的最小值;若不存在,请说明理由.


 B.
B.
 D.
D.





 粤公网安备 44130202000953号
粤公网安备 44130202000953号