2019年福建省中考数学试卷
如图是某班甲、乙、丙三位同学最近5次数学成绩及其所在班级相应平均分的折线统计图,则下列判断错误的是

| A. |
甲的数学成绩高于班级平均分,且成绩比较稳定 |
| B. |
乙的数学成绩在班级平均分附近波动,且比丙好 |
| C. |
丙的数学成绩低于班级平均分,但成绩逐次提高 |
| D. |
就甲、乙、丙三个人而言,乙的数学成绩最不稳 |
《增删算法统宗》记载:"有个学生资性好,一部孟子三日了,每日增添一倍多,问君每日读多少?"其大意是:有个学生天资聪慧,三天读完一部《孟子》,每天阅读的字数是前一天的两倍,问他每天各读多少个字?已知《孟子》一书共有34685个字,设他第一天读 个字,则下面所列方程正确的是
| A. |
|
B. |
|
| C. |
|
D. |
|
某校征集校运会会徽,遴选出甲、乙、丙三种图案.为了解何种图案更受欢迎,随机调查了该校100名学生,其中60名同学喜欢甲图案,若该校共有2000人,根据所学的统计知识可以估计该校喜欢甲图案的学生有 人.
如图,边长为2的正方形 中心与半径为2的 的圆心重合, 、 分别是 、 的延长线与 的交点,则图中阴影部分的面积是 .(结果保留

已知 和点 ,如图.
(1)以点 为一个顶点作△ ,使△ ,且△ 的面积等于 面积的4倍;(要求:尺规作图,不写作法,保留作图痕迹)
(2)设 、 、 分别是 三边 、 、 的中点, 、 、 分别是你所作的△ 三边 、 、 的中点,求证: △ .
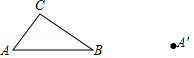
在 中, , ,将 绕点 顺时针旋转一定的角度 得到 ,点 、 的对应点分别是 、 .
(1)当点 恰好在 上时,如图1,求 的大小;
(2)若 时,点 是边 中点,如图2,求证:四边形 是平行四边形.
某工厂为贯彻落实"绿水青山就是金山银山"的发展理念,投资组建了日废水处理量为 吨的废水处理车间,对该厂工业废水进行无害化处理.但随着工厂生产规模的扩大,该车间经常无法完成当天工业废水的处理任务,需要将超出日废水处理量的废水交给第三方企业处理.已知该车间处理废水,每天需固定成本30元,并且每处理一吨废水还需其他费用8元;将废水交给第三方企业处理,每吨需支付12元.根据记录,5月21日,该厂产生工业废水35吨,共花费废水处理费370元.
(1)求该车间的日废水处理量 ;
(2)为实现可持续发展,走绿色发展之路,工厂合理控制了生产规模,使得每天废水处理的平均费用不超过10元 吨,试计算该厂一天产生的工业废水量的范围.
某种机器使用期为三年,买方在购进机器时,可以给各台机器分别一次性额外购买若干次维修服务,每次维修服务费为2000元.每台机器在使用期间,如果维修次数未超过购机时购买的维修服务次数,每次实际维修时还需向维修人员支付工时费500元;如果维修次数超过购机时购买的维修服务次数,超出部分每次维修时需支付维修服务费5000元,但无需支付工时费.某公司计划购买1台该种机器,为决策在购买机器时应同时一次性额外购买几次维修服务,搜集并整理了100台这种机器在三年使用期内的维修次数,整理得下表;
维修次数 |
8 |
9 |
10 |
11 |
12 |
频数(台数) |
10 |
20 |
30 |
30 |
10 |
(1)以这100台机器为样本,估计"1台机器在三年使用期内维修次数不大于10"的概率;
(2)试以这100台机器维修费用的平均数作为决策依据,说明购买1台该机器的同时应一次性额外购10次还是11次维修服务?
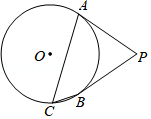
如图,四边形 内接于 , , ,垂足为 ,点 在 的延长线上,且 ,连接 、 .
(1)求证: ;
(2)若 , ,求 的值.








 粤公网安备 44130202000953号
粤公网安备 44130202000953号