2016年江苏省淮安市中考数学试卷
在“市长杯”足球比赛中,六支参赛球队进球数如下(单位:个) ,5,6,2,5,1,这组数据的众数是
A.5B.6C.4D.2
如图,在 中, ,以顶点 为圆心,适当长为半径画弧,分别交 , 于点 , ,再分别以点 , 为圆心,大于 的长为半径画弧,两弧交于点 ,作射线 交边 于点 ,若 , ,则 的面积是
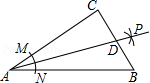
A.15B.30C.45D.60
一个不透明的袋子中装有3个黄球和4个蓝球,这些球除颜色外完全相同,从袋子中随机摸出一个球,摸出的球是黄球的概率是 .
如图,在 中, , , ,点 在边 上,并且 ,点 为边 上的动点,将 沿直线 翻折,点 落在点 处,则点 到边 距离的最小值是 .

王师傅检修一条长600米的自来水管道,计划用若干小时完成,在实际检修过程中,每小时检修管道长度是原计划的1.2倍,结果提前2小时完成任务,王师傅原计划每小时检修管道多少米?
如图,转盘 的三个扇形面积相等,分别标有数字1,2,3,转盘 的四个扇形面积相等,分别有数字1,2,3,4.转动 、 转盘各一次,当转盘停止转动时,将指针所落扇形中的两个数字相乘(当指针落在四个扇形的交线上时,重新转动转盘).
(1)用树状图或列表法列出所有可能出现的结果;
(2)求两个数字的积为奇数的概率.

为了丰富同学们的课余生活,某学校举行“亲近大自然”户外活动,现随机抽取了部分学生进行主题为“你最想去的景点是?”的问卷调查,要求学生只能从“ (植物园), (花卉园), (湿地公园), (森林公园)”四个景点中选择一项,根据调查结果,绘制了如下两幅不完整的统计图.

请解答下列问题:
(1)本次调查的样本容量是 ;
(2)补全条形统计图;
(3)若该学校共有3600名学生,试估计该校最想去湿地公园的学生人数.
小宇想测量位于池塘两端的 、 两点的距离.他沿着与直线 平行的道路 行走,当行走到点 处,测得 ,再向前行走100米到点 处,测得 .若直线 与 之间的距离为60米,求 、 两点的距离.

如图,在 中, ,点 在边 上,以点 为圆心, 为半径的圆经过点 ,过点 作直线 ,使 .
(1)判断直线 与 的位置关系,并说明理由;
(2)若 , ,求图中阴影部分的面积.

甲、乙两家草莓采摘园的草莓品质相同,销售价格也相同.“五一期间”,两家均推出了优惠方案,甲采摘园的优惠方案是:游客进园需购买60元的门票,采摘的草莓六折优惠;乙采摘园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,设某游客的草莓采摘量为 (千克),在甲采摘园所需总费用为 (元 ,在乙采摘园所需总费用为 (元 ,图中折线 表示 与 之间的函数关系.
(1)甲、乙两采摘园优惠前的草莓销售价格是每千克 元;
(2)求 、 与 的函数表达式;
(3)在图中画出 与 的函数图象,并写出选择甲采摘园所需总费用较少时,草莓采摘量 的范围.

如图,在平面直角坐标系中,二次函数 的图象与坐标轴交于 、 、 三点,其中点 的坐标为 ,点 的坐标为 .
(1)求该二次函数的表达式及点 的坐标;
(2)点 的坐标为 ,点 为该二次函数在第一象限内图象上的动点,连接 、 ,以 、 为邻边作平行四边形 ,设平行四边形 的面积为 .
①求 的最大值;
②在点 的运动过程中,当点 落在该二次函数图象上时,请直接写出此时 的值.

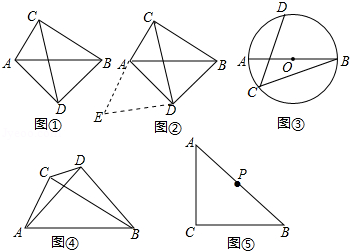
问题背景:
如图①,在四边形 中, , ,探究线段 , , 之间的数量关系.
小吴同学探究此问题的思路是:将 绕点 ,逆时针旋转 到 处,点 , 分别落在点 , 处(如图② ,易证点 , , 在同一条直线上,并且 是等腰直角三角形,所以 ,从而得出结论: .
简单应用:
(1)在图①中,若 , ,则 .
(2)如图③, 是 的直径,点 、 在 上, ,若 , ,求 的长.
拓展规律:
(3)如图④, , ,若 , ,求 的长(用含 , 的代数式表示)
(4)如图⑤, , ,点 为 的中点,若点 满足 , ,点 为 的中点,则线段 与 的数量关系是 .
 B.
B. C.
C. D.
D.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号