2019年内蒙古呼和浩特市中考数学试卷
如图,检测排球,其中质量超过标准的克数记为正数,不足的克数记为负数,下面检测过的四个排球,在其上方标注了检测结果,其中质量最接近标准的一个是( )

| A. |
|
B. |
|
C. |
|
D. |
|
甲骨文是我国的一种古代文字,下面是"北""比""鼎.射"四个字的甲骨文,其中不是轴对称图形的是( )
| A. |
|
B. |
|
| C. |
|
D. |
|
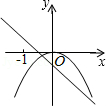
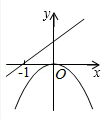
二次函数 y= ax 2与一次函数 y= ax+ a在同一坐标系中的大致图象可能是( )
| A. |
|
B. |
|
| C. |
|
D. |
|
已知菱形的边长为3,较短的一条对角线的长为2,则该菱形较长的一条对角线的长为( )
| A. |
2 |
B. |
2 |
C. |
4 |
D. |
2 |
某学校近几年来通过"书香校园"主题系列活动,倡导学生整本阅读纸质课外书籍.下面的统计图是该校2013年至2018年纸质书人均阅读量的情况,根据统计图提供的信息,下列推断不合理的是( )

| A. |
从2013年到2016年,该校纸质书人均阅读量逐年增长 |
| B. |
2013年至2018年,该校纸质书人均阅读量的中位数是46.7本 |
| C. |
2013年至2018年,该校纸质书人均阅读量的极差是45.3本 |
| D. |
2013年至2018年,该校后三年纸质书人均阅读量总和是前三年纸质书人均阅读量总和的2倍 |
若不等式 ﹣1≤2﹣ x的解集中 x的每一个值,都能使关于 x的不等式3( x﹣1)+5>5 x+2( m+ x)成立,则 m的取值范围是( )
| A. |
m>﹣ |
B. |
m<﹣ |
C. |
m<﹣ |
D. |
m>﹣ |
如图是一个几何体的三视图,其中主视图与左视图完全一样,则这个几何体的表面积是( )

| A. |
80﹣2π |
B. |
80+4π |
C. |
80 |
D. |
80+6π |
若 x 1, x 2是一元二次方程 x 2+ x﹣3=0的两个实数根,则 x 2 3﹣4 x 1 2+17的值为( )
| A. |
﹣2 |
B. |
6 |
C. |
﹣4 |
D. |
4 |
已知正方形的对称中心在坐标原点,顶点 A、 B、 C、 D按逆时针依次排列,若 A点的坐标为(2, ),则 B点与 D点的坐标分别为( )
| A. |
(﹣2, ),(2,﹣ ) |
B. |
(﹣ ,2),( ,﹣2) |
| C. |
(﹣ ,2),(2,﹣ ) |
D. |
(- , )( , ) |
以下四个命题:①用换元法解分式方程- =1时,如果设 = y,那么可以将原方程化为关于 y的整式方程 y 2+ y﹣2=0;②如果半径为 r的圆的内接正五边形的边长为 a,那么 a=2 rcos54°;③有一个圆锥,与底面圆直径是 且体积为 的圆柱等高,如果这个圆锥的侧面展开图是半圆,那么它的母线长为 ;④二次函数 y= ax 2﹣2 ax+1,自变量的两个值 x 1, x 2对应的函数值分别为 y 1、 y 2,若| x 1﹣1|>| x 2﹣1|,则 a( y 1﹣ y 2)>0.其中正确的命题的个数为( )
| A. |
1个 |
B. |
2个 |
C. |
3个 |
D. |
4个 |
下面三个命题:①底边和顶角对应相等的两个等腰三角形全等;②两边及其中一边上的中线对应相等的两个三角形全等;③斜边和斜边上的中线对应相等的两个直角三角形全等,其中正确的命题的序号为 .
已知正方形 ABCD的面积是2, E为正方形一边 BC在从 B到 C方向的延长线上的一点,若 CE= ,连接 AE,与正方形另外一边 CD交于点 F,连接 BF并延长,与线段 DE交于点 G,则 BG的长为 .
如图,在△ ABC中,内角 A、 B、 C所对的边分别为 a、 b、 c.
(1)若 a=6, b=8, c=12,请直接写出∠ A与∠ B的和与∠ C的大小关系;
(2)求证:△ ABC的内角和等于180°;
(3)若 ,求证:△ ABC是直角三角形.
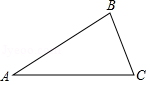
如图,已知甲地在乙地的正东方向,因有大山阻隔,由甲地到乙地需要绕行丙地.已知丙地位于甲地北偏西30°方向,距离甲地460 km,丙地位于乙地北偏东66°方向,现要打通穿山隧道,建成甲乙两地直达高速公路,如果将甲、乙、丙三地当作三个点 A、 B、 C,可抽象成图(2)所示的三角形,求甲乙两地之间直达高速线路的长 AB(结果用含非特殊角的三角函数和根式表示即可).

镇政府想了解对王家村进行"精准扶贫"一年来村民的经济情况,统计员小李用简单随机抽样的方法,在全村130户家庭中随机抽取20户,调查过去一年的收入(单位:万元),从而去估计全村家庭年收入情况.
已知调查得到的数据如下:
1.9,1.3,1.7,1.4,1.6,1.5,2.7,2.1,1.5,0.9,2.6,2.0,2.1,1.0,1.8,2.2,2.4,3.2,1.3,2.8
为了便于计算,小李在原数据的每个数上都减去1.5,得到下面第二组数:
0.4,﹣0.2,0.2,﹣0.1,0.1,0,1.2,0.6,0,﹣0.6,1.1,0.5,0.6,﹣0.5,0.3,0.7,0.9,1.7,﹣0.2,1.3
(1)请你用小李得到的第二组数计算这20户家庭的平均年收入,并估计全村年收入及全村家庭年收入超过1.5万元的百分比;已知某家庭过去一年的收入是1.89万元,请你用调查得到的数据的中位数推测该家庭的收入情况在全村处于什么水平?
(2)已知小李算得第二组数的方差是 S,小王依据第二组数的方差得出原数据的方差为(1.5+ S) 2,你认为小王的结果正确吗?如果不正确,直接写出你认为正确的结果.
滴滴快车是一种便捷的出行工具,计价规则如下表:
计费项目 |
里程费 |
时长费 |
远途费 |
单价 |
1.8元/公里 |
0.3元/分钟 |
0.8元/公里 |
注:车费由里程费、时长费、远途费三部分构成,其中里程费按行车的实际里程计算;时长费按行车的实际时间计算;远途费的收取方式为:行车里程7公里以内(含7公里)不收远途费,超过7公里的,超出部分每公里收0.8元. |
|||
小王与小张各自乘坐满滴快车,在同一地点约见,已知到达约见地点时他们的实际行车里程分别为6公里与8.5公里,两人付给滴滴快车的乘车费相同.
(1)求这两辆滴滴快车的实际行车时间相差多少分钟;
(2)实际乘车时间较少的人,由于出发时间比另一人早,所以提前到达约见地点在大厅等候.已知他等候另一人的时间是他自己实际乘车时间的1.5倍,且比另一人的实际乘车时间的一半多8.5分钟,计算俩人各自的实际乘车时间.
如图,在平面直角坐标系中,矩形 OCAB( OC> OB)的对角线长为5,周长为14.若反比例函数 y= 的图象经过矩形顶点 A.
(1)求反比例函数解析式;若点(﹣ a, y 1)和( a+1, y 2)在反比例函数的图象上,试比较 y 1与 y 2的大小;
(2)若一次函数 y= kx+ b的图象过点 A并与 x轴交于点(﹣1,0),求出一次函数解析式,并直接写出 kx+ b﹣ <0成立时,对应 x的取值范围.

如图,以Rt△ ABC的直角边 AB为直径的⊙ O交斜边 AC于点 D,过点 D作⊙ O的切线与 BC交于点 E,弦 DM与 AB垂直,垂足为 H.
(1)求证: E为 BC的中点;
(2)若⊙ O的面积为12π,两个三角形△ AHD和△ BMH的外接圆面积之比为3,求△ DEC的内切圆面积 S 1和四边形 OBED的外接圆面积 S 2的比.

已知二次函数 y= ax 2﹣ bx+ c且 a= b,若一次函数 y= kx+4与二次函数的图象交于点 A(2,0).
(1)写出一次函数的解析式,并求出二次函数与 x轴交点坐标;
(2)当 a> c时,求证:直线 y= kx+4与抛物线 y= ax 2﹣ bx+ c一定还有另一个异于点 A的交点;
(3)当 c< a≤ c+3时,求出直线 y= kx+4与抛物线 y= ax 2﹣ bx+ c的另一个交点 B的坐标;记抛物线顶点为 M,抛物线对称轴与直线 y= kx+4的交点为 N,设 S= S △ AMN﹣ S △ BMN,写出 S关于 a的函数,并判断 S是否有最大值?如果有,求出最大值;如果没有,请说明理由.








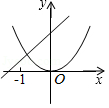

 粤公网安备 44130202000953号
粤公网安备 44130202000953号