2018年内蒙古兴安盟中考数学试卷(a卷)
下列计算结果正确的是( )
| A. |
3+ =3 |
| B. |
(m﹣n)(m 2+mn+n 2)=m 3﹣n 3 |
| C. |
(﹣2b 2) 3=﹣6b 6 |
| D. |
(﹣a) 2•a 6=﹣a 8 |
如图,是一个长方体的主视图与左视图,由图示数据(单位: cm)可得出该长方体的体积是( )

| A. |
9cm 3 |
B. |
8cm 3 |
C. |
6 cm 3 |
D. |
18 cm 3 |
已知一组数据4,0,﹣3,6,2,﹣1,则这组数据的中位数是( )
| A. |
0 |
B. |
﹣3 |
C. |
2 |
D. |
1 |
如图, AB∥ CD,∠ C=70°,∠ A=40°,则∠ F的度数为( )

| A. |
30° |
B. |
35° |
C. |
40° |
D. |
45° |
如图,在平面直角坐标系中,以 O为圆心,适当长为半径画弧,交 x轴于点 M,交 y轴于点 N,再分别以点 M, N为圆心,大于 MN的长为半径画弧,两弧在第二象限交于点 P,若点 P的坐标为(3 a, b+1),则 a与 b的数量关系为( )
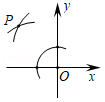
| A. |
3a=2b |
B. |
3a=b+1 |
C. |
3a+b﹣1=0 |
D. |
3a=﹣b﹣1 |
在平面直角坐标系中,点 A的坐标为(1, ),以原点 O为中心,将点 A顺时针旋转60°得到点 A',则点 A′的坐标为( )
| A. |
(0, ) |
B. |
(1,﹣ ) |
C. |
(﹣1, ) |
D. |
(2,0) |
若式子 +( m﹣1) 0有意义,则一次函数 y=( m﹣1) x+1﹣ m的图象可能( )
| A. |
|
B. |
|
| C. |
|
D. |
|
如图,在扇形 AOB中,∠ AOB=90°,正方形 CDEF的顶点 C是 的中点,点 D在 OB上,点 E在 OB的延长线上,当正方形 CDEF的边长为3 时,则阴影部分的面积为( )

| A. |
18﹣ π |
B. |
π﹣9 |
C. |
π﹣9 |
D. |
π﹣18 |
如图,已知 A( , y 1), B(2, y 2)为反比例函数 y= 图象上的两点,动点 P( x,0)在 x轴的正半轴上运动,当线段 AP与线段 BP之差达到最大时点 P的坐标是( )

| A. |
( ,0) |
B. |
(3,0) |
C. |
(4,0) |
D. |
( ,0) |
为了考察甲、乙两种小麦的长势,某农研所科技人员,分别从中随机抽取10株麦苗,测得苗高(单位: cm)如下表:
甲 |
10 |
12 |
12 |
14 |
11 |
13 |
14 |
12 |
11 |
11 |
乙 |
10 |
11 |
13 |
12 |
12 |
11 |
13 |
14 |
12 |
12 |
则 种小麦的长势比较整齐.(填"甲"或"乙")
如图,在矩形 ABCD中, AB=8, BC=6, M为 AD上一点,将△ ABM沿 BM翻折至△ EBM, ME和 BE分别与 CD相交于 O, F两点,且 OE= OD,则 AM的长为 .

一艘轮船在静水中的最大航速为30 km/ h,它以最大航速沿江顺流航行90 km所用时间,与以最大航速逆流航行60 km所用时间相等,江水的流速为多少?
如图,矩形 ABCD中,过对角线 BD中点 O的直线分别交 AB, CD边于点 E、 F.
(1)求证:四边形 BEDF是平行四边形;
(2)只需添加一个条件,即 ,可使四边形 BEDF为菱形.

如图为甲、乙两个可以自由转动的均匀的转盘,甲转盘被分成3个面积相等的扇形,乙转盘被分成4个面积相等的扇形,每一个扇形都标有相应的数字,同时转动两个转盘,当转盘停止后,设甲转盘中指针所指区域内的数字为 m,乙转盘中指针所指区域内的数字为 n(若指针指在边界线上时,重转一次,直到指针指向一个区域为止)
(1)请你用画树状图或列表的方法求出 m和 n的乘积为偶数的概率;
(2)直接写出点( m, n)落在函数 y=﹣4 x图象上的概率.

如图,在梯形 ABCD中, AD∥ BC,∠ ADC=90°,∠ B=30°, CE⊥ AB,垂足为点 E.若 AD=1, AB=4 ,求△ BCE外接圆的面积.

为了了解某市八年级学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,某记者开展了一次抽样调査,根据调查结果绘制了如下尚不完整的统计图

根据以上信息解答下列问题
(1)这次接受调查的八年级学生总人数为多少?
(2)扇形统计图中"动画"对应扇形的圆心角度数为多少?
(3)请补全条形统计图.
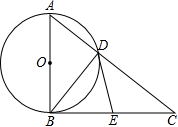
如图,在△ ABC中,∠ ABC=90°,以 AB的中点 O为圆心, OA为半径的圆交 AC于点 D, E是 BC的中点,连结 DE、 OE.
(1)判断 DE与⊙ O的位置关系,并说明理由.
(2)求证: BC 2=2 CD• OE.
某厂商投产一种新型科技产品,每件制造成本为18元,试销过程中发现,每月销售量 y(万件)与销售单价 x(元)之间的关系可以近似地看作一次函数 y=﹣2 x+100
(1)写出每月的利润 L(万元)与销售单价 x(元)之间的函数关系式;
(2)当销售单价为多少元时,厂商每月能获得312万元的利润?当销售单价为多少元时,厂商每月能获得最大利润?最大利润是多少?
(3)根据相关部门规定,这种科技产品的销售单价不能高于32元,如果厂商要获得每月不低于312万元的利润,那么制造出这种产品每月的最低制造成本需要多少万元?





 粤公网安备 44130202000953号
粤公网安备 44130202000953号