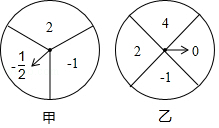
如图为甲、乙两个可以自由转动的均匀的转盘，甲转盘被分成3个面积相等的扇形，乙转盘被分成4个面积相等的扇形，每一个扇形都标有相应的数字，同时转动两个转盘，当转盘停止后，设甲转盘中指针所指区域内的数字为 m，乙转盘中指针所指区域内的数字为 n（若指针指在边界线上时，重转一次，直到指针指向一个区域为止）

（1）请你用画树状图或列表的方法求出 m和 n的乘积为偶数的概率；

（2）直接写出点（ m， n）落在函数 y＝﹣4 x图象上的概率．