2020年吉林省中考数学试卷
国务院总理李克强2020年5月22日在作政府工作报告时说,去年我国农村贫困人口减少11090000,脱贫攻坚取得决定性成就.数据11090000用科学记数法表示为
| A. |
|
B. |
|
C. |
|
D. |
|
我国古代数学著作《算学启蒙》中有这样一个数学问题,其大意是:跑得快的马每天走240里,跑得慢的马每天走150里,慢马先走12天,快马几天可以追上慢马?设快马 天可以追上慢马,根据题意,可列方程为 .
如图,某单位要在河岸 上建一个水泵房引水到 处.他们的做法是:过点 作 于点 ,将水泵房建在了 处.这样做最节省水管长度,其数学道理是 .

如图,在四边形 中, , ,我们把这种两组邻边分别相等的四边形叫做“筝形”.筝形 的对角线 , 相交于点 .以点 为圆心, 长为半径画弧,分别交 , 于点 , .若 , ,则 的长为 (结果保留 .

"中国结"是我国特有的手工编织工艺品,也是一种传统吉祥装饰物.如图,现有三张正面印有"中国结"图案的不透明卡片 , , ,卡片除正面图案不同外,其余均相同.将三张卡片正面向下洗匀,小吉同学从中随机抽取一张卡片,记下图案后正面向下放回,洗匀后再从中随机抽取一张卡片,请用画树状图或列表的方法,求小吉同学抽出的两张卡片中含有 卡片的概率.

甲、乙二人做某种机械零件.已知甲每小时比乙多做6个,甲做90个所用的时间与乙做60个所用的时间相等.求乙每小时做零件的个数.
图①、图②、图③都是 的正方形网格,每个小正方形的顶点称为格点. , , 均为格点.在给定的网格中,按下列要求画图:
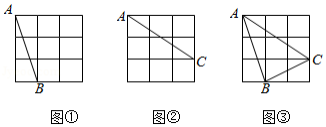
(1)在图①中,画一条不与 重合的线段 ,使 与 关于某条直线对称,且 , 为格点.
(2)在图②中,画一条不与 重合的线段 ,使 与 关于某条直线对称,且 , 为格点.
(3)在图③中,画一个 ,使 与 关于某条直线对称,且 , , 为格点.
如图,某班数学小组测量塔的高度,在与塔底部 相距 的 处,用高 的测角仪 测得该塔顶端 的仰角 为 .求塔 的高度(结果精确到 .
(参考数据: , ,

如图,在平面直角坐标系中, 为坐标原点,点 , 在函数 的图象上(点 的横坐标大于点 的横坐标),点 的坐标为 ,过点 作 轴于点 ,过点 作 轴于点 ,连接 , .
(1)求 的值.
(2)若 为 中点,求四边形 的面积.

2020年3月线上授课期间,小莹、小静和小新为了解所在学校九年级600名学生居家减压方式情况,对该校九年级部分学生居家减压方式进行抽样调查.将居家减压方式分为 (享受美食)、 (交流谈心)、 (室内体育活动)、 (听音乐)和 (其他方式)五类,要求每位被调查者选择一种自己最常用的减压方式.他们将收集的数据进行了整理,绘制的统计表分别为表1、表2和表3.
表1:小莹抽取60名男生居家减压方式统计表(单位:人)
减压方式 |
|
|
|
|
|
人数 |
4 |
6 |
37 |
8 |
5 |
表2:小静随机抽取10名学生居家减压方式统计表(单位:人)
减压方式 |
|
|
|
|
|
人数 |
2 |
1 |
3 |
3 |
1 |
表3:小新随机抽取60名学生居家减压方式统计表(单位:人)
减压方式 |
|
|
|
|
|
人数 |
6 |
5 |
26 |
13 |
10 |
根据以上材料,回答下列问题:
(1)小莹、小静和小新三人中,哪一位同学抽样调查的数据能较好地反映出该校九年级学生居家减压方式情况,并简要说明其他两位同学抽样调查的不足之处.
(2)根据三人中能较好地反映出该校九年级居家减压方式的调查结果,估计该校九年级600名学生中利用室内体育活动方式进行减压的人数.
某种机器工作前先将空油箱加满,然后停止加油立即开始工作.当停止工作时,油箱中油量为 ,在整个过程中,油箱里的油量 (单位: 与时间 (单位: 之间的关系如图所示.
(1)机器每分钟加油量为 ,机器工作的过程中每分钟耗油量为 .
(2)求机器工作时 关于 的函数解析式,并写出自变量 的取值范围.
(3)直接写出油箱中油量为油箱容积的一半时 的值.

能够完全重合的平行四边形纸片 和 按图①方式摆放,其中 , .点 , 分别在边 , 上, 与 相交于点 .
【探究】求证:四边形 是菱形.
【操作一】固定图①中的平行四边形纸片 ,将平行四边形纸片 绕着点 顺时针旋转一定的角度,使点 与点 重合,如图②.则这两张平行四边形纸片未重叠部分图形的周长和为 .
【操作二】将图②中的平行四边形纸片 绕着点 继续顺时针旋转一定的角度,使点 与点 重合,连接 , ,如图③,若 ,则四边形 的面积为 .

如图, 是等边三角形, ,动点 从点 出发,以 的速度沿 向点 匀速运动,过点 作 ,交折线 于点 ,以 为边作等边三角形 ,使点 , 在 异侧.设点 的运动时间为 , 与 重叠部分图形的面积为 .
(1) 的长为 (用含 的代数式表示).
(2)当点 落在边 上时,求 的值.
(3)求 关于 的函数解析式,并写出自变量 的取值范围.











 粤公网安备 44130202000953号
粤公网安备 44130202000953号