2020年湖北省襄阳市中考数学试卷
下列说法正确的是
| A. |
"买中奖率为 的奖券10张,中奖"是必然事件 |
| B. |
"汽车累积行驶 ,从未出现故障"是不可能事件 |
| C. |
襄阳气象局预报说"明天的降水概率为 ",意味着襄阳明天一定下雨 |
| D. |
若两组数据的平均数相同,则方差小的更稳定 |
我国古代数学名著《孙子算经》中记载了一道题,大意是:100匹马恰好拉了100片瓦,已知3匹小马能拉1片瓦,1匹大马能拉3片瓦,求小马,大马各有多少匹.若设小马有 匹,大马有 匹,则下列方程组中正确的是
| A. |
|
B. |
|
| C. |
|
D. |
|
已知四边形 是平行四边形, , 相交于点 ,下列结论错误的是
| A. |
, |
| B. |
当 时,四边形 是菱形 |
| C. |
当 时,四边形 是矩形 |
| D. |
当 且 时,四边形 是正方形 |
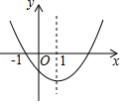
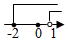
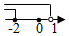
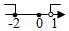
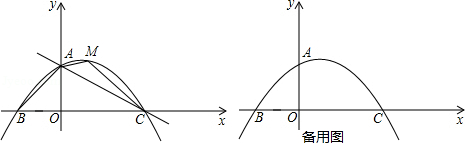
二次函数 的图象如图所示,下列结论:
① ;② ;③ ;④当 时, 随 的增大而减小.
其中正确的有
| A. |
4个 |
B. |
3个 |
C. |
2个 |
D. |
1个 |
《易经》是中国传统文化的精髓.如图是易经的一种卦图,图中每一卦由三根线组成(线形为 或
或 ,如正北方向的卦为
,如正北方向的卦为 ,从图中三根线组成的卦中任取一卦,这一卦中恰有2根
,从图中三根线组成的卦中任取一卦,这一卦中恰有2根 和1根
和1根 的概率为 .
的概率为 .

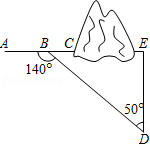
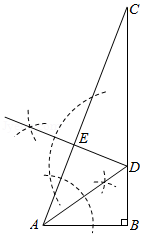
襄阳东站的建成运营标志着我市正式进入高铁时代,郑万高速铁路襄阳至万州段的建设也正在推进中.如图,工程队拟沿 方向开山修路,为加快施工进度,需在小山的另一边点 处同时施工.要使 、 、 三点在一条直线上,工程队从 上的一点 取 , 米, .那么点 与点 间的距离是多少米?
(参考数据: , ,
在襄阳市创建全国文明城市的工作中,市政部门绿化队改进了对某块绿地的灌浇方式.改进后,现在每天用水量是原来每天用水量的 ,这样120吨水可多用3天,求现在每天用水量是多少吨?
3月14日是国际数学日,"数学是打开科学大门的钥匙."为进一步提高学生学习数学的兴趣,某校开展了一次数学趣味知识竞赛(竞赛成绩为百分制),并随机抽取了50名学生的竞赛成绩(本次竞赛没有满分),经过整理数据得到以下信息:
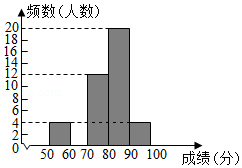
信息一:50名学生竞赛成绩频数分布直方图如图所示,从左到右依次为第一组到第五组(每组数据含前端点值,不含后端点值).
信息二:第三组的成绩(单位:分)为74 71 73 74 79 76 77 76 76 73 72 75
根据信息答案下列问题:
(1)补全第二组频数分布直方图(直接在图中补全);
(2)第三组竞赛成绩的众数是 分,抽取的50名学生竞赛成绩的中位数是 分;
(3)若该校共有1500名学生参赛,请估计该校参赛学生成绩不低于80分的约为 人.
如图,反比例函数 和一次函数 的图象都经过点 和点 .
(1) , ;
(2)求一次函数的解析式,并直接写出 时 的取值范围;
(3)若点 是反比例函数 的图象上一点,过点 作 轴,垂足为 ,则 的面积为 .
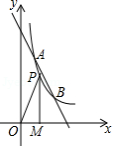
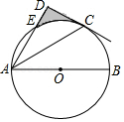
如图, 是 的直径, , 是 上两点,且 ,连接 , .过点 作 交 的延长线于点 .
(1)判定直线 与 的位置关系,并说明理由;
(2)若 , ,求图中阴影部分的面积.
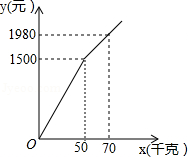
受新冠肺炎疫情影响,一水果种植专业户有大量成熟水果无法出售."一方有难,八方支援"某水果经销商主动从该种植专业户购进甲,乙两种水果进行销售.专业户为了感谢经销商的援助,对甲种水果的出售价格根据购买量给予优惠,对乙种水果按25元 千克的价格出售.设经销商购进甲种水果 千克,付款 元, 与 之间的函数关系如图所示.
(1)直接写出当 和 时, 与 之间的函数关系式;
(2)若经销商计划一次性购进甲,乙两种水果共100千克,且甲种水果不少于40千克,但又不超过60千克.如何分配甲,乙两种水果的购进量,才能使经销商付款总金额 (元 最少?
(3)若甲,乙两种水果的销售价格分别为40元 千克和36元 千克.经销商按(2)中甲,乙两种水果购进量的分配比例购进两种水果共 千克,且销售完 千克水果获得的利润不少于1650元,求 的最小值.
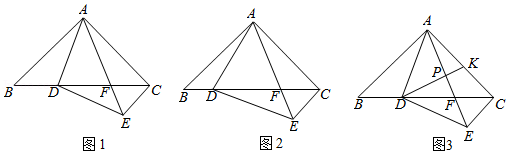
在 中, , ,点 在边 上, 且 , 交边 于点 ,连接 .
(1)特例发现:如图1,当 时,
①求证: ;
②推断: ;
(2)探究证明:如图2,当 时,请探究 的度数是否为定值,并说明理由;
(3)拓展运用:如图3,在(2)的条件下,当 时,过点 作 的垂线,交 于点 ,交 于点 ,若 ,求 的长.



 粤公网安备 44130202000953号
粤公网安备 44130202000953号