2016年天津市中考数学试卷
2016年5月24日《天津日报》报道,2015年天津外环线内新栽植树木6120000株,将6120000用科学记数法表示应为
| A. |
|
B. |
|
C. |
|
D. |
|
已知二次函数 为常数),在自变量 的值满足 的情况下,与其对应的函数值 的最小值为5,则 的值为
| A. |
1或 |
B. |
或5 |
C. |
1或 |
D. |
1或3 |
不透明袋子中装有6个球,其中有1个红球、2个绿球和3个黑球,这些球除颜色外无其他差别,从袋子中随机取出1个球,则它是绿球的概率是 .
如图,在每个小正方形的边长为1的网格中, , 为格点, , 为小正方形边的中点, 为 , 的延长线的交点.
(Ⅰ) 的长等于 ;
(Ⅱ)若点 在线段 上,点 在线段 上,且满足 ,请在如图所示的网格中,用无刻度的直尺,画出线段 ,并简要说明点 , 的位置是如何找到的(不要求证明) .

解不等式 ,请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得 ;
(Ⅱ)解不等式②,得 ;
(Ⅲ)把不等式①和②的解集在数轴上表示出来;
(Ⅳ)原不等式组的解集为 .
在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位: ,绘制出如下的统计图①和图②,请根据相关信息,解答下列问题:

(Ⅰ)图1中 的值为 ;
(Ⅱ)求统计的这组初赛成绩数据的平均数、众数和中位数;
(Ⅲ)根据这组初赛成绩,由高到低确定9人进入复赛,请直接写出初赛成绩为 的运动员能否进入复赛.
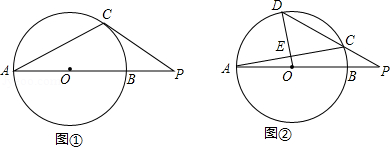
在 中, 为直径, 为 上一点.
(Ⅰ)如图1.过点 作 的切线,与 的延长线相交于点 ,若 ,求 的大小;
(Ⅱ)如图2, 为 上一点,且 经过 的中点 ,连接 并延长,与 的延长线相交于点 ,若 ,求 的大小.
小明上学途中要经过 , 两地,由于 , 两地之间有一片草坪,所以需要走路线 , ,如图,在 中, , , ,求 , 的长.(结果保留小数点后一位)
参考数据: , , , 取1.414.

公司有330台机器需要一次性运送到某地,计划租用甲、乙两种货车共8辆,已知每辆甲种货车一次最多运送机器45台、租车费用为400元,每辆乙种货车一次最多运送机器30台、租车费用为280元
(Ⅰ)设租用甲种货车 辆 为非负整数),试填写表格.
表一:
租用甲种货车的数量 辆 |
3 |
7 |
|
租用的甲种货车最多运送机器的数量 台 |
135 |
|
|
租用的乙种货车最多运送机器的数量 台 |
150 |
|
|
表二:
租用甲种货车的数量 辆 |
3 |
7 |
|
租用甲种货车的费用 元 |
|
2800 |
|
租用乙种货车的费用 元 |
|
280 |
|
(Ⅱ)给出能完成此项运送任务的最节省费用的租车方案,并说明理由.
在平面直角坐标系中, 为原点,点 ,点 ,把 绕点 逆时针旋转,得△ ,点 , 旋转后的对应点为 , ,记旋转角为 .
(Ⅰ)如图①,若 ,求 的长;
(Ⅱ)如图②,若 ,求点 的坐标;
(Ⅲ)在(Ⅱ)的条件下,边 上 的一点 旋转后的对应点为 ,当 取得最小值时,求点 的坐标(直接写出结果即可)













 粤公网安备 44130202000953号
粤公网安备 44130202000953号