江苏省南京市鼓楼区九年级上学期期中考试数学试卷

方程x²=x的解是（    ）

一组数据5，2，5，3，2．5，5，5，5．5，这7个数据的众数和中位数分别是（    ）

沅江市近年来大力发展芦笋产业，某芦笋生产企业在两年内的销售额从20万元增加到80万元．设这两年的销售额的年平均增长率为x，根据题意可列方程为（    ）

有一组数据如下：3，a，4，6，7，它们的平均数是5，那么这组数据的方差是（    ）

A．

B．2

C．

D．10

如图，四边形ABCD为⊙O的内接四边形，已知∠BOD=100°，则∠BCD的度数为（    ）

如图，⊙O的内接四边形ABCD两组对边的延长线分别交于点E，F，∠E=α，∠F=β，则∠A=（    ）

A．α+β

B．

C．180-α-β

D．

写出一个解为1和2的一元二次方程：                    ．

已知⊙O的半径是3，OP=2，则点P与⊙O的位置关系是：点P在⊙O              ．

如果关于x的一元二次方程x²+4x-m=0没有实数根，那么m的取值范围是          ．

小明上学期平时成绩为90分，其中成绩为88分，期末成绩为94分，若平时、期中、期末的成绩按3：3：4计算，计算结果作为学期成绩，则小明上学期学期成绩为       分．

已知一元二次方程x²-6x-5=0的两根为m，n，则m²-mn+n²=                 ．

已知⊙A的半径是6，点A的坐标是（-3，-4），那么⊙A与x轴的位置关系是        ．

将圆心角为90°，面积为4π的扇形围成一个圆锥的侧面，则所围成的圆锥的底面半径为                      ．

如图，AB为⊙O直径，点C，D在⊙O上，若∠DCB=30°，则∠DBA=             ．

将量角器按如图所示的方式放置在三角形纸片上，使点O在半圆上，点B在半圆上，边AB，AO分别交半圆于点C，D，点B，C，D对应的读数分别为160°、52°、40°，则∠A=       ．

同圆的内接正方形和内接正三角形的边长比是                  ．

（1）解方程：
①x²-6x-4=0     
②x²-12x+27=0
（2）直接写出方程（x²-6x-4）（x²-12x+27）=0的解为                            ．

为了从甲、乙两名射击运动员中选拔一名参加比赛，对这两名运动员进行测试，他们10次射击命中的环数如下：

 
根据测试成绩，你认为选择哪一名运动员参赛更好？为什么？

已知△ABC，∠C=90°，AC=4，BC=3．
（1）用尺规在图1中作出△ABC的外接圆，在图2中作出△ABC的内切圆．
（2）△ABC的外接圆半径为        ，内切圆半径为         ．

已知关于x的方程kx²+（2k+1）x+2=0．
（1）若方程有两个不相等的实数根，则k的取值范围是              ；
（2）求证：无论k取任何实数时，方程总有实数根．

如图，四边形ABCD内接于⊙O，∠DAE是四边形ABCD的一个外角，且AD平分∠CAE．
求证：DB=DC．

如图，⊙O是△ABC的外接圆，半径为4，直线l与⊙O相切，切点为P，l∥BC，l与BC间的距离为7．

（1）仅用无刻度的直尺，画出一条弦，使这条炫将△ABC分成面积相等的两部分（保留作图痕迹，不写画法）．
（2）求弦BC的长．

如图，在△ABC中，AB=AC，∠ABC=30°，点O在边BC上，⊙O经过点A，B，且与BC相交于点D．

（1）求证：CA是⊙O的切线；
（2）若AB=2，请直接写出阴影部分的面积．

某水产店每天购进一种高档海鲜500千克，预计每千克盈利10元，当天可全部售完，经市场调查发现，在进货价不变的情况下，若每千克涨价1元，日销售量将减少20千克．当天剩余的海鲜全部以每千克盈利5元的价格卖给某饭店，如果该水产店要保证当天盈利6500元，那么每千克应涨价多少元？

某课题小组研究如下的几个问题．
（1）边长为1的等边三角形从图1位置开始沿直线顺时针无滑动地向右滚动一周，求点P运动的路径长（直接列式计算）；
（2）边长为1的正方形从图2位置开始沿直线顺时针无滑动地向右滚动，当正方形滚动一周时，求点P运动的路经长（直接列式计算）．
（3）请你将（1）（2）中的正多边形化成一个边长为1，边数大于4的正多边形，按（1）（2）的方式滚动一周，求其任意一个顶点运动的路径长（请写出你选的图形的名称，直接写出结果）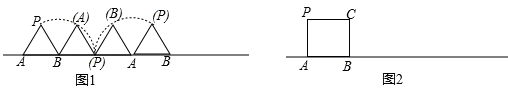

要建一个面积为150m²的长方形养鸡场，为了节省材料，养鸡场的一边靠着原有的一条墙，墙长am，另三边用竹篱笆围成．如果篱笆的总长为40m，设养鸡场垂直于墙的一边长为xm，求养鸡场的长和宽．

如图，在平面直角坐标系中，直线l的表达式是y=-x+1，长度为2的线段AB在y轴上移动，设点A的坐标为（0，a）．

（1）当以A为圆心，AB为半径的圆与直线l相切时，求a的值；
（2）直线l上若存在点C，使得△ABC是以AB为腰的等腰三角形，则a的取值范围为        ；
（3）直线l上是否存在点C，使得∠ACB=90°？若存在，求出a的取值范围；若不存在，请说明理由．