辽宁省沈阳市指南针教育高一上第一次月考数学试卷
设集合S=|x|x<﹣1或x>5},T={x|a<x<a+8},且S∪T=R,则实数a的取值范围是( )
| A.﹣3<a<﹣1 | B.﹣3≤a≤﹣1 |
| C.a≤﹣3或a≥﹣1 | D.a<﹣3或a>﹣1 |
设全集 ,则∁UM=( )
,则∁UM=( )
| A.∅ | B.{(2,3)} | C.(2,3) | D.{2,3} |
下列函数f(x)与g(x)表示同一函数的是( )
| A.f(x)=x0与g(x)=1 |
B.f(x)=x与g(x)=(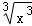 ) ) |
C.f(x)=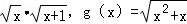 |
D.f(x)=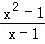 ,g(x)=x+1 ,g(x)=x+1 |
设f(x)在(﹣∞,+∞)上是减函数,且a+b≤0,则下列各式成立的是( )
| A.f(a)+f(b)≤0 |
| B.f(a)+f(b)≥0 |
| C.f(a)+f(b)≤f(﹣a)+f(﹣b) |
| D.f(a)+f(b)≥f(﹣a)+f(﹣b) |
设集合M={x|﹣1≤x<2},N={x|x﹣k≤0},若M∩N=M,则k的取值范围( )
| A.(﹣1,2) | B.[2,+∞) |
| C.(2,+∞) | D.[﹣1,2] |
设函数f(x)和g(x)分别是R上的偶函数和奇函数,则下列结论恒成立的是( )
| A.f(x)+|g(x)|是偶函数 |
| B.f(x)﹣|g(x)|是奇函数 |
| C.|f(x)|+g(x)是偶函数 |
| D.|f(x)|﹣g(x)是奇函数 |
定义两种运算:a⊕b= ,a⊗b=
,a⊗b= ,则函数
,则函数 为( )
为( )
| A.奇函数 | B.偶函数 |
| C.奇函数且为偶函数 | D.非奇函数且非偶函数 |
已知函数f(x)是定义在R上的奇函数,若对于任意给定的不等实数x1,x2,不等式x1f(x1)+x2f(x2)<x1f(x2)+x2f(x1)恒成立,则不等式f(1﹣x)<0的解集为( )
| A.(﹣∞,0) | B.(0,+∞) | C.(﹣∞,1) | D.(1,+∞) |
偶函数f(x)(x∈R)满足:f(﹣4)=f(1)=0,且在区间[0,3]与[3,+∞)上分别递减和递增,则不等式x3f(x)<0的解集为( )
| A.(﹣∞,﹣4)∪(4,+∞) |
| B.(﹣4,﹣1)∪(1,4) |
| C.(﹣∞,﹣4)∪(﹣1,0) |
| D.(﹣∞,﹣4)∪(﹣1,0)∪(1,4) |
下列四个说法:
(1)函数f(x)>0在x>0时是增函数,x<0也是增函数,所以f(x)是增函数;
(2)若函数f(x)=ax2+bx+2与x轴没有交点,则b2﹣8a<0且a>0;
(3)y=x2﹣2|x|﹣3的递增区间为[1,+∞);
(4)y=1+x和 表示相等函数.
表示相等函数.
其中说法正确的个数是( )
| A.0 | B.1 | C.2 | D.3 |
若定义在[﹣2013,2013]上的函数f(x)满足:对于任意的x1,x2∈[﹣2013,2013],有f(x1+x2)=f(x1)+f(x2)﹣2012,且x>0时,有f(x)>2012,f(x)的最大、小值分别为M、N,则M+N的值为( )
| A.2011 | B.2012 | C.4022 | D.4024 |
对于实数a,b,定义运算“⊗”:a⊗b= ,设f(x)=(2x﹣1)⊗(x﹣1),且关于x的方程f(x)﹣m=0恰有三个互不相等的实数根,则实数m的取值范围是 .
,设f(x)=(2x﹣1)⊗(x﹣1),且关于x的方程f(x)﹣m=0恰有三个互不相等的实数根,则实数m的取值范围是 .
已知集合A={x|x2﹣x﹣2>0},函数g(x)= 的定义域为集合B,
的定义域为集合B,
(1)求A∩B和A∪B;
(2)若C={x|4x+p<0},且C⊆A,求实数P的取值范围.
已知函数f(x)的定义域为(﹣2,2),函数g(x)=f(x﹣1)+f(3﹣2x).
(1)求函数g(x)的定义域;
(2)若f(x)是奇函数且在定义域内单调递减,求不等式g(x)≤0的解集.
已知二次函数f(x)满足条件:f(0)=1,f(x+1)=f(x)+2x
(Ⅰ)求f(x);
(Ⅱ)讨论二次函数f(x)在闭区间[t,t+1](t∈R)上的最小值.
 ,则f(2x﹣1)的定义域为( )
,则f(2x﹣1)的定义域为( )



 的定义域是 .
的定义域是 . 若f(2﹣a2)>f(a),则实数a的取值范围为 .
若f(2﹣a2)>f(a),则实数a的取值范围为 . >0成立.
>0成立. ]恒成立,求m的取值范围.
]恒成立,求m的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号