期中备考总动员高三理数学模拟卷【新课标2】3
高三 班共有学生
班共有学生 人,现根据座号,用系统抽样的方法,抽取一个容量为
人,现根据座号,用系统抽样的方法,抽取一个容量为 的样本.已知
的样本.已知 号、
号、 号、
号、 号同学在样本中,那么样本中还有一个同学的座号是( )
号同学在样本中,那么样本中还有一个同学的座号是( )
A. |
B. |
C. |
D. |
执行如图所示的程序框图,若输出 的值为16,那么输入的
的值为16,那么输入的 值等于( )
值等于( )

| A.5 | B.6 | C.7 | D.8 |
同时具有性质“⑴最小正周期是 ;⑵图象关于直线
;⑵图象关于直线 对称;⑶ 在
对称;⑶ 在 上是减函数”的一个函数可以是( )
上是减函数”的一个函数可以是( )
A. |
B. |
C. |
D. |
已知 位选手依次演讲,其中选手甲不在第一个也不在最后一个演讲,则不同的演讲次序共有( )
位选手依次演讲,其中选手甲不在第一个也不在最后一个演讲,则不同的演讲次序共有( )
A. 种 种 |
B. 种 种 |
C. 种 种 |
D. 种 种 |
【改编】设椭圆的方程为 右焦点为
右焦点为 ,方程
,方程 的两实根分别为
的两实根分别为 ,则
,则 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
一个四面体的顶点在空间直角坐标系 中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的主视图时,以
中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的主视图时,以 平面为投影面,则得到主视图可以为( )
平面为投影面,则得到主视图可以为( )

已知球 的直径
的直径 ,
, 是球
是球 球面上的三点,
球面上的三点, 是正三角形,且
是正三角形,且 ,则三棱锥
,则三棱锥 的体积为 ( )
的体积为 ( )
A. |
B. |
C. |
D. |
在平面直角坐标系 中,已知圆
中,已知圆 ,圆
,圆 均与
均与 轴相切且圆心
轴相切且圆心 ,
, 与原点
与原点 共线,
共线, ,
, 两点的横坐标之积为6,设圆
两点的横坐标之积为6,设圆 与圆
与圆 相交于
相交于 ,
, 两点,直线
两点,直线 :
: ,则点
,则点 与直线
与直线 上任意一点
上任意一点 之间的距离的最小值为 .
之间的距离的最小值为 .
(本小题满分12分)如图,在四棱锥 中,
中, 平面
平面 ,
, ,四边形
,四边形 满足
满足 ,
, 且
且 ,点
,点 为
为 中点,点
中点,点 为
为 边上的动点,且
边上的动点,且 .
.
(1)求证:平面 平面
平面 ;
;
(2)是否存在实数 ,使得二面角
,使得二面角 的余弦值为
的余弦值为 ?若存在,试求出实数
?若存在,试求出实数 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(本小题满分12分)口袋中装有除颜色,编号不同外,其余完全相同的2个红球,4个黑球.现从中同时取出3个球.
(Ⅰ)求恰有一个黑球的概率;
(Ⅱ)记取出红球的个数为随机变量 ,求
,求 的分布列和数学期望
的分布列和数学期望 .
.
已知椭圆 的上顶点为
的上顶点为 ,直线
,直线 交椭圆于
交椭圆于 两点,设直线
两点,设直线 的斜率分别为
的斜率分别为 .
.
(1)若 时,求
时,求 的值;
的值;
(2)若 时,证明直线
时,证明直线 过定点.
过定点.
(本小题满分10分)选修4-4:坐标系与参数方程
已知圆锥曲线 (
( 为参数)和定点
为参数)和定点 ,
, 、
、 是此圆锥曲线的左、右焦点,以原点
是此圆锥曲线的左、右焦点,以原点 为极点,以
为极点,以 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求直线 的直角坐标方程;
的直角坐标方程;
(2)经过点 且与直线
且与直线 垂直的直线
垂直的直线 交此圆锥曲线于
交此圆锥曲线于 、
、 两点,求
两点,求 的值.
的值.
 ,
, ,则
,则 ( )
( )



 的共轭复数为 ( )
的共轭复数为 ( )



 为等差数列
为等差数列 的前
的前 项和,若
项和,若 ,公差
,公差 ,
, ,则
,则 ( )
( ) ,
, 满足
满足 ,则
,则 的取值范围是( )
的取值范围是( )



 的导函数
的导函数 ,且
,且 ,则函数
,则函数 的零点个数为( )
的零点个数为( ) ,则
,则 的值是( )
的值是( )



 对一切
对一切 都有
都有 ,且当
,且当 时,
时, ,则当
,则当 时,
时, 的最大值为 .
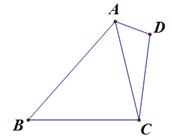
的最大值为 . 中,
中,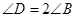 ,且
,且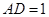 ,
,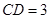 ,
, .
.
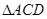 的面积;
的面积;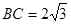 ,求
,求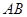 的长.
的长. ,
, .
. 时,证明:
时,证明: ;
; ,若
,若 ,求a的取值范围.
,求a的取值范围. 中,
中, 是
是 的角平分线,
的角平分线, 的外接圆交
的外接圆交 于点
于点 ,
, .
.
 ;
; ,
, 时,求
时,求 的长.
的长. 的解集为
的解集为 ,
, .
. ;
; 与
与 的大小,并说明理由.
的大小,并说明理由. 粤公网安备 44130202000953号
粤公网安备 44130202000953号