山东省济南市高三上学期期末考试理科数学试卷
“ ”是“函数
”是“函数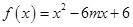 在区间
在区间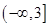 上为减函数”的
上为减函数”的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分又不必要条件 |
在某项测量中,测量结果X服从正态分布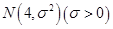 ,若X在(0,8)内取值的概率为0.6,则X在(0,4)内取值的概率为
,若X在(0,8)内取值的概率为0.6,则X在(0,4)内取值的概率为
| A.0.2 | B.0.3 | C.0.4 | D.0.6 |
点A是抛物线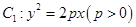 与双曲线
与双曲线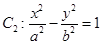
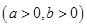 的一条渐近线的交点,若点A到抛物线
的一条渐近线的交点,若点A到抛物线 的准线的距离为p,则双曲线
的准线的距离为p,则双曲线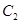 的离心率等于
的离心率等于
A.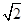 |
B.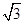 |
C. |
D. |
已知圆C过点 ,且圆心在x轴的负半轴上,直线
,且圆心在x轴的负半轴上,直线 被该圆所截得的弦长为
被该圆所截得的弦长为 ,则过圆心且与直线l平行的直线方程为________.
,则过圆心且与直线l平行的直线方程为________.
已知命题:
①将一组数据中的每个数都变为原来的2倍,则方差也变为原来的2倍;
②命题“ ”的否定是“
”的否定是“ ”;
”;
③在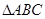 中,若
中,若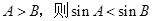 ;
;
④在正三棱锥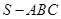 内任取一点P,使得
内任取一点P,使得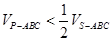 的概率是
的概率是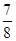 ;
;
⑤若对于任意的 恒成立,则实数a的取值范围是
恒成立,则实数a的取值范围是 .
.
以上命题中正确的是__________(填写所有正确命题的序号).
(本小题满分12分)在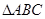 中,角A,B,C的对边分别为
中,角A,B,C的对边分别为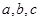 ,且
,且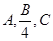 成等差数列.
成等差数列.
(I)若 的值;
的值;
(II)设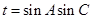 ,求t的最大值.
,求t的最大值.
(本小题满分12分)为了参加市中学生运动会,某校从四支较强的班级篮球队A,B,C,D中选出12人组成校男子篮球队,队员来源如下表:
(I)从这12名队员中随机选出两名,求两人来自同一个队的概率;
(II)比赛结束后,学校要评选出3名优秀队员(每一个队员等可能被评为优秀队员),设其中来自A队的人数为 ,求随机变量
,求随机变量 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)在四棱锥 ,
,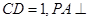 平面ABCD,PA=2.
平面ABCD,PA=2.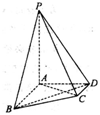
(I)设平面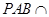 平面
平面 ,求证:
,求证: ;
;
(II)设点Q为线段PB上一点,且直线QC与平面PAC所成角的正切值为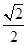 ,求
,求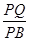 的值.
的值.
(本小题满分12分)已知等比数列 的前n项和为
的前n项和为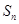 ,且满足
,且满足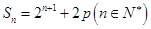 .
.
(I)求p的值及数列 的通项公式;
的通项公式;
(II)若数列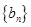 满足
满足 ,求数列
,求数列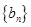 的前n项和
的前n项和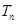 .
.
(本小题满分13分)已知椭圆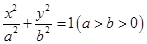 的离心率为
的离心率为 ,且过点
,且过点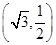 .
.
(I)求椭圆的标准方程;
(II)四边形ABCD的顶点在椭圆上,且对角线AC,BD过原点O,设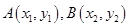 ,满足
,满足 .
.
(i)试证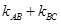 的值为定值,并求出此定值;
的值为定值,并求出此定值;
(ii)试求四边形ABCD面积的最大值.
 是纯虚数,则
是纯虚数,则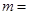

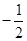

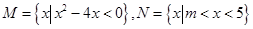 ,若
,若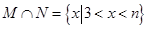 ,则
,则 等于
等于




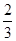



 的图象向左平移
的图象向左平移 个单位,得到函数
个单位,得到函数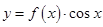 的图象,则
的图象,则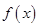 的表达式可以是
的表达式可以是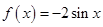


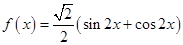
 图象的是
图象的是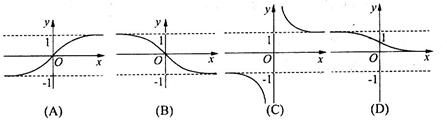
 中,
中, 是AB中点,且对于边AB上任一点P,恒有
是AB中点,且对于边AB上任一点P,恒有 ,则有
,则有

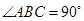

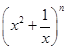 的二项展开式的各项系数和为32,则二项展开式中含
的二项展开式的各项系数和为32,则二项展开式中含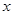 项的系数为________.
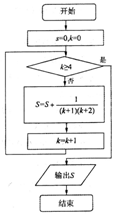
项的系数为________.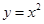 和曲线
和曲线 围成的图形的面积是________.
围成的图形的面积是________.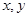 满足约束条件
满足约束条件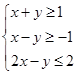 ,若目标函数
,若目标函数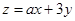 仅在点(1,0)处取得最小值,则a的取值范围为_________.
仅在点(1,0)处取得最小值,则a的取值范围为_________. .
.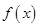 在点
在点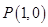 处的切线方程;
处的切线方程; 上,函数
上,函数 的上方,试求a的最大值.
的上方,试求a的最大值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号