湖南省株洲市高三教学质量统一检测一文科数学试卷
设数列{an}是等比数列,函数y=x2-x-2的两个零点是 ,则
,则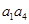 =( )
=( )
| A.2 | B.1 | C.-1 | D.-2 |
已知条件p:k= ;条件q:直线y= kx+2与圆x2+y2=1相切,则p是q的( )
;条件q:直线y= kx+2与圆x2+y2=1相切,则p是q的( )
| A.充分不必要条件 |
| B.必要不充分条件 |
| C.充分必要条件 |
| D.既不充分也不必要条件 |
下列函数中,与函数y=-3|x|的奇偶性相同,且在(-∞,0)上
单调性也相同的是( )
A.y=- |
B.y=log2|x| | C.y=1-x2 | D.y=x3-1 |
在长方体ABCD A1B1C1D1中,AB=BC=2,AA1=1,则BC1与平面BB1D1D所成角的正弦值为( )
A. |
B.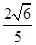 |
C.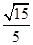 |
D. |
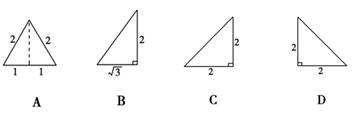
已知三棱锥的正视图与俯视图如图所示,俯视图是边长为2的正三角形,则该三棱锥的侧视图可能为( )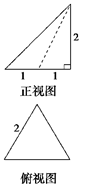
已知双曲线 的一条渐近线的倾斜角的余弦值为
的一条渐近线的倾斜角的余弦值为 ,该双曲线上过一个焦点且垂直于实轴的弦长为
,该双曲线上过一个焦点且垂直于实轴的弦长为 ,则双曲线的离心率等于( )
,则双曲线的离心率等于( )
A. |
B. |
C. |
D. |
在 中,若角
中,若角 所对的三边
所对的三边 成等差数列,给出下列结论:
成等差数列,给出下列结论:
① ;②
;② ;③
;③ ;④
;④ .
.
其中正确的结论是( )
| A.①② | B.②③ | C.③④ | D.①④ |
记集合 和集合
和集合 表示的平
表示的平
面区域分别为Ω1,Ω2,若在区域Ω1内任取一点M(x,y),则点M落在区域Ω2内的概率
为 .
如图,在第一象限内,矩形ABCD的三个顶点A,B,C分别在函数y= 的图像上,且矩形的边分别平行两坐标轴,若A点的纵坐标是2,则D点的坐标是
的图像上,且矩形的边分别平行两坐标轴,若A点的纵坐标是2,则D点的坐标是 
海关对同时从A,B,C三个不同地区进口的某种商品进行抽样检测,从各地区进口此种商品的数量(单位:件)如下表所示. 工作人员用分层抽样的方法从这些商品中共抽取6件样品进行检测.
| 地区 |
A |
B |
C |
| 数量 |
50 |
150 |
100 |
(Ⅰ)求这6件样品中来自A,B,C各地区商品的数量;
(Ⅱ)若在这6件样品中随机抽取2件送往甲机构进行进一步检测,求这2件商品来自相同地区的概率.
已知数列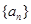 是各项均为正数的等差数列,其中
是各项均为正数的等差数列,其中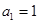 ,且
,且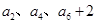 成等比数列;数列
成等比数列;数列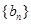 的前
的前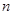 项和为
项和为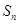 ,满足
,满足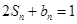 .
.
(1)求数列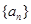 、
、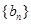 的通项公式;
的通项公式;
(2)如果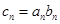 ,设数列
,设数列 的前
的前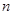 项和为
项和为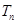 ,是否存在正整数
,是否存在正整数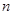 ,使得
,使得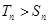 成立,若存在,求出
成立,若存在,求出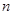 的最小值,若不存在,说明理由.
的最小值,若不存在,说明理由.
如图,点 分别是椭圆C:
分别是椭圆C: 的左、右焦点,过点
的左、右焦点,过点 作
作 轴的垂线,交椭圆
轴的垂线,交椭圆 的上半部分于点
的上半部分于点 ,过点
,过点 作
作 的垂线交直线
的垂线交直线 于点
于点 .
.
(1)如果点 的坐标为(4,4),求椭圆
的坐标为(4,4),求椭圆 的方程;
的方程;
(2)试判断直线 与椭圆
与椭圆 的公共点个数,并证明你的结论.
的公共点个数,并证明你的结论.
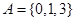 ,
,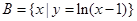 ,则
,则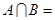 ( )
( )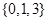
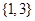

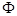
 ,
, ”的否定是( )
”的否定是( ) ,
,






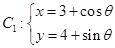 (
(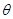 为参数)上,则|AB|的最大值为 .
为参数)上,则|AB|的最大值为 . ,
, ,且
,且 ∥
∥ ,则
,则
 中,
中,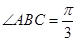 ,对角线
,对角线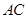 与
与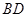 相交于
相交于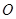 ,点
,点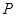 是线段
是线段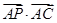 等于 .
等于 . .
. 时,求函数
时,求函数 的最大值;
的最大值; ,求
,求 的值.
的值. 中,底面
中,底面 为正方形,
为正方形, //
// //
// ,
, ,且
,且 .
.
 //
// ;
; .
.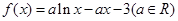
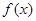 的单调性;
的单调性;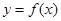 的图象在点
的图象在点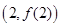 处的切线的倾斜角为
处的切线的倾斜角为 ,对于任意的
,对于任意的 ,函数
,函数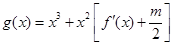 在区间
在区间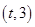 上总不是单调函数,求
上总不是单调函数,求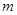 的取值范围;
的取值范围;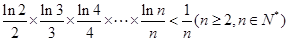
 粤公网安备 44130202000953号
粤公网安备 44130202000953号