高中物理探究单摆的周期与摆长的关系试题

如图所示，放置在水平地面上的支架质量为M，支架顶端用细线拴着的摆球质量为m，现将摆球拉至水平位置，而后释放，摆球运动过程中，支架始终不动，以下说法正确的是（ ）

A．在释放前的瞬间，支架对地面的压力为（m+M）g

B．在释放前的瞬间，支架对地面的压力为mg

C．摆球到达最低点时，支架对地面的压力为（m+M）g

D．摆球到达最低点时，支架对地面的压力为（3m+M）g

在地球表面上周期准确的秒摆（周期为2秒），移到距离地面为nR₀的高度处（R₀为地球半径），该秒摆的周期    秒，此时为了让秒摆保持周期2秒不变，则需要    (“增长”，“减短”）摆长．

实验小组用细线做了如下实验，请完成填空：
 
将细线一端固定，另一端系在弹簧测力计挂钩上，水平拉细线，缓慢增大拉力，当测力计示数如图甲时，细线刚好拉断。该细线能承受的最大拉力为        N；
用螺旋测微器测量一金属球的直径，读数如图乙，则该金属球直径为         m；
用天平测出该金属球的质量m =" 100.0" g；
用完全相同的细线与该小球做成一个摆，细线上端固定在O 点，如图丙，测出线长，再加上小球的半径，得到悬点O 到小球球心的距离为1.0000 m。
在悬点O 的正下方A 点钉上一个光滑的钉子，再将小球拉起至细线水平且绷直，由静止释放小球，摆至竖直时，细线碰到钉子，为使细线不断裂，A 与O 的距离应满足的条件是：      。（取g =" 9.8" m/s2,不计空气阻力）

如图所示，一对杂技演员（都视为质点）乘秋千（秋千绳处于水平位置）从A点由静止出发绕O点下摆，当摆到最低点B时，女演员在极短时间内将男演员沿水平方向推出，然后自己刚好能回到高处A。求男演员落地点C与O点的水平距离。已知男演员质量和女演员质量之比，秋千的质量不计，秋千的摆长为R，C点比O点低。

两个摆长相同的单摆，摆球质量之比是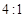，在不同地域振动，当甲摆振动4次的同时，乙摆恰振动5次，则甲、乙二摆所在地区重力加速度之比为        。

单摆在周期在下列何种情况时会增大（  ）

A．增大摆球质量

B．减小摆长

C．把单摆从赤道移到北极

D．把单摆从海平面移到高山

将一单摆向右拉至水平标志线上，从静止释放，当摆球运动到最低点时，摆线碰到障碍物，摆球继续向左摆动，用频闪照相机拍到如图所示的单摆运动过程的频闪照片，摆球从最高点M摆至左边最高点N时，以下说法正确的是（   ）

A．摆线碰到障碍物前后的摆长之比为

B．摆线碰到障碍物前后的摆长之比为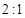

C．摆线经过最低点时，线速度不变，半径减小，摆线张力变大

D．摆线经过最低点时，角速度不变，半径减小，摆线张力变大

关于机械振动和机械波，下列说法正确的是

A．有机械振动必有机械波

B．声音在空气中传播时是横波

C．在机械波的传播中质点并不随波迁移

D．质点的振动方向与波的传播方向总在同一直线上

如图所示，单摆摆球的质量为m，摆长为L，摆球从最大位移A处由静止释放，摆球运动到最低点B时的速度大小为v。重力加速度为g，不计空气阻力。则摆球从A运动到B的过程中

A．重力做的功为

B．重力的最大瞬时功率为mgv

C．重力的功率先增大后减小

D．摆球运动到最低点B时绳的拉力为

(13分)动画片《熊出没》中有这样一个情节：某天熊大和熊二中了光头强设计的陷阱， 被挂在了树上，聪明的熊大想出了一个办法，让自己和熊二荡起来使绳断裂从而得救，其过程可简化如图所示，设悬点为0，离地高度为H=6m，两熊可视为质点且总质量m=500kg，重心为A，荡下过程重心到悬点的距离L=2m且保持不变，绳子能承受的最大张力为T=10⁴N，光头强（可视为质点）位于距离0点水平距离s=5m的B点处，不计一切阻力，重力加速度g=10m/s²。

（1）熊大和熊二为了解救自己，荡至最高点时绳与竖直方向的夹角α至少为多大？
（2）设熊大和熊二刚好在向右摆到最低点时绳子断裂，则他们的落地点离光头强的距离为多少？
（3）如果重心A到0的距离可以改变，且两熊向右摆到最低点时绳子恰好断裂，有无可能在落地时砸中光头强？请通过计算说明。

一振动周期为T，振幅为A，位于x=0点的波源从平衡位置沿y轴正向开始做简谐振动，该波源产生的一维简谐横波沿x轴正向传播，波速为v，传播过程中无能量损失，一段时间后，该振动传播至某质点P，关于质点P振动的说法正确的是______。（填正确答案标号，选对1个得2分，选对2个得4分，选对3个得5分。每选错1个扣3分，最低得分为0分）

A．振幅一定为A

B．周期一定为T

C．速度的最大值一定为v

D．开始振动的方向沿y轴向上

E．开始振动的方向沿y轴向上或向下取决于它离波源的距离

做简谐振动的单摆摆长不变，若摆球质量增加为原来的4倍，摆球经过平衡位置时速度减小为原来的1/2，则单摆振动的(     )

A．频率、振幅都不变	B．频率、振幅都改变
C．频率不变、振幅改变	D．频率改变、振幅不变

一个弹簧振子，第一次被压缩x后释放做自由振动，周期为T₁，第二次被压缩2x后释放做自由振动，周期为T₂，则两次振动周期之比T₁∶T₂为（   ）

A．1∶2

B．1∶1

C．2∶1

D．1∶4

、将秒摆（周期为2 s）的周期变为1 s，下列措施可行的是（  ）

A．将摆球的质量减半

B．振幅减半

C．摆长减为原来的1/4

D．摆长减半

下列说法正确的是(    )

A．摆钟偏快时可缩短摆长进行校准

B．火车鸣笛向我们驶来时，我们听到的笛声频率将比声源发声的频率高

C．拍摄玻璃橱窗内的物品时，往往在镜头前加一个偏振片以增加透射光的强度

D．地面附近有一高速水平飞过的火箭，地面上的人观察到的火箭长度要比火箭上的人观察到的短一些

E．光从水中射入玻璃中，发现光线偏向法线，则光在玻璃中传播速度一定小于在水中的传播速度